Aurélie 12/09/07
 

Etude du filtre passe bas concours technicien laboratoire 2007

En poursuivant votre navigation sur ce site, vous acceptez l’utilisation de Cookies vous proposant des publicités adaptés à vos centres d’intérêts.

. .
.
.

On fixe R1=R2=R et C1=C2=C

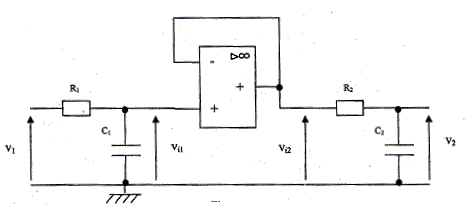
On suppose que le filtre fonctionne en régime sinusoïdal à la pulsation w.

Les quatre tensions v1(t), vi1(t), v2(t), vi2(t) étant sinusoïdales, on leur associe les grandeurs complexes respectives V1, V i1,V2, V i2.

Déterminer l'expression du rapport V i1 / V 1, en fonction de R, C et w.

réponse :

V1i = 1/(jCw) i d'où i =V1i jCw

V1= V1i +R i = (R +1/(jCw) ) i

remplacer i par son expression :

V1= (R +1/(jCw) ) V1i jCw= (jRCw +1 ) V1i = (1+jRCw ) V1i

V i1 / V 1 = 1/ [1+jCR w ].
Quel est le rôle de l'étage intermédiaire à amplificateur opérationnel ? Que vaut le rapport V i2 / V 1 ?

réponse :

Le montage avec A.O est un montage suiveur donc V i2 / V 1 = V i1 / V 1 = 1/ [1+jCR w ].

Le montage suiveur permet de réaliser un générateur de tension parfait.

Exprimer le rapport V2 / V i2 en fonction de R, C et w.

réponse :

V2 = 1/(jCw) i d'où i =V2 jCw

Vi2= V2 +R i = (R +1/(jCw) ) i

remplacer i par son expression :

Vi2= (R +1/(jCw) ) V2 jCw= (jRCw +1 ) V2 = (1+jRCw ) V2

V 2 / V i2 = 1/ [1+jCR w ].

Exprimer la fonction de transfert F= V2 / V1 du filtre en fonction des rapports V2 / V i2 , Vi2 / V i1 , V i1/ V1

En déduire l'expression de F en fonction de RC et w.

réponse :

V2 / V1 = V2 / V i2 * V i2/ V i1 * V i1/ V1 avec V i2/ V i1 =1.

V2 / V1 =1/ [1+jCR w ]2.

Montrer que F peut s'écrire F= 1/[1+j f/f0]2 avec f0 = 1/(2pRC).

réponse :

w = 2 p f avec f fréquence en Hz.

RC w = 2RC p f = f/f0 avec f0 = 1/(2pRC).

d'où F= 1/[1+j f/f0]2

 

 
Montrer que la fréquence de coupure fc à -3 dB est telle que fc=0,64 f0.

 réponse :

On cherche le module de F= 1/[1+j f/f0]2 en posant f/f0 = x.

F= (1-jx)2 / [(1+jx)2(1-jx)2] = (1-jx)2 / (1+x2)2 = (1-x2-2jx) / (1+x2)2

module de F=[(1-x2)2 + 4x2)]½ / (1+x2)2 = (1+x2) / (1+x2)2

module de F=G = 1/(1+x2)

GdB = 20 log G = 20 log [1/(1+x2)] = -20 log(1+x2)

La fréquence de coupure d'un filtre est la fréquence pour laquelle le signal de sortie est atténué de -10 log2 dB ( environ -3dB ) :

-3 =-20 log(1+x2) ; log(1+x2) = 3/20 = 0,15 ; 1+x2 = 1,41

x2 = 0,41 ; x= 0,64 soit fc/f0 =0,64 ou fc = 0,64 f0.

On fixe C= 1mF. Calculer R pour avoir fc=1 Hz.

f0 = 1/(2pRC) ; fc = 0,64 f0 ; fc = 0,64/(2pRC)

fc2pRC = 0,64 ; R = 0,64 / (fc2pC)

R= 0,64 / (6,28*10-6) =1,0 105 W.

On applique v1(t) = V1+V1a sin( 2pft) avec f = 100 Hz.

Déterminer l'expression approchée de v2(t). Quel est le rôle du filtre ? 

réponse :

V2 = V1 / [1+j f/f0]2 avec f0 = 1/(2pRC) = 1/(2*3,14*105*10-6) =1,6 Hz.

Pour la composante continue V1, f=0 et le module de F vaut 1/(1+(f/f0)2)= 1.

Pour la composante V1a sin( 2pft), f= 100 Hz et le module de F vaut : 1/(1+(100/1,6)2) = 3 10-4 voisin de zéro

Le filtre laisse passer les très basses fréquences et élimine les fréquences moyennes et élevées : filtre passe bas.
retour -menu