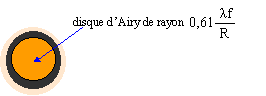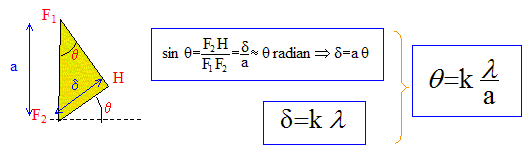|
Propriétés du laser, diffraction, interférences concours technicien laboratoire 2007 En poursuivant votre navigation sur ce site, vous acceptez l’utilisation de Cookies vous proposant des publicités adaptés à vos centres d’intérêts. |
|
| .
. |
|
|
|
|
Le rayonnement laser :
Dl<< l : la lumière laser est pratiquement monochromatique. Fréquence moyenne n de la radiation : n =c / l = 3,00 108 / 633 10-9 = 4,74 1014 Hz ; couleur jaune. Ouverture du faisceau :
r = 2,00 * 1,00 10-3 = 2,00 10-3 m diamètre de la tache circulaire : 4,00 10-3 m. surface éclairée s= p r2 = 3,14 *(2,00 10-3)2 = 1,26 10-5 m2. Le faisceau laser est très directif. Eclairement en W m-2 : P/s = 1,0 10-3 / 1,26 10-5 = 80 W m-2. 12 fois inférieur à l'éclairement en plein soleil en été. Mais bien supérieur au seuil d'exposition maximal tolérable pour l'oeil : il ne faut pas diriger le faisceau laser vers les yeux. Le faisceau laser a une grande puissance par unité de surface.
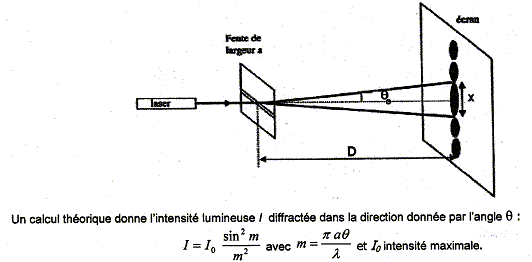
Diffraction à l'infini par une ouverture rectangulaire ( fente) : On réalise le montage ci-dessous :
On observe sur l'écran une tache centrale intense entourée de taches latérales beaucoup moins lumineuses : les franges de diffraction.
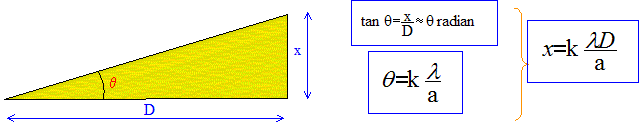
Expression de la largeur angulaire a = 2q0 de la frange centrale : L'intensité lumineuse est nulle si sin m = 0 avec m différent de zéro soit m = ( 2k+1) p avec k un nombre entier p aq/l = ( 2k+1) p ; q = ( 2k+1)l / a. si k = 0 : q0 = l / a ; a = 2q0 =2l / a. Expression de la largeur x de la tache centrale sur l'écran : tan q0 = 0,5 x / D voisin de q0 radian. 2q0 = x / D = 2l /a d'où x = 2lD /a. x = 633 10-9 * 2 *4,90 / 100 10-6 = 6,20 10-2 m = 6,20 cm. ax = 2lD = constante ; si a augmente alors x diminue d'autant. a et x sont inversement
proportionnelles.
I/I0 = sin2m / m2 avec m = (2k+1) ½p au centre des franges brillantes. ordre 1 , k=1 et m = 1,5 p. I/I0 = sin2(1,5 p) / (1,5 p)2 = 1/(1,5 p)2 ; I/I0 =0,045. La seconde frange brillante est bien moins visible que la frange centrale ; les franges d'ordre supérieur deviennent rapidement invisibles. Epaisseur de ce cheveux : x = 2 l D/ épaisseur ; épaisseur = 2 l D/ x épaisseur = 2*633 10-9 * 4,90 / 3,00 10-2 = 2,07 10-4 m = 207 mm. Figure de diffraction donnée par une ouverture circulaire :
|
|
|
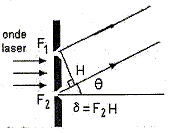
On remplace la fente unique par un système de deux fentes identiques parallèles de largeur L=90 mm écartées de a= 175 m m ( entre axes).
On observe alors sur l'écran des zones équidistantes alternativement sombres et brillantes. Quel nom donne t-on à ce phénomène ? interférences. On interprète le phénomène comme la superposition de 2 ondes lumineuses diffractées par chacune des deux fentes F1 et F2 dans la direction donnée par l'angle q.
Donner l'expression de la différence de marche d=F2H en fonction de a=F1F2 et q. On montre que l'onde résultante de la superposition précédente présente une amplitude maximale si la différence de marche est un multiple entier de la longueur d'onde d = kl avec k entier. Donner l'expression des valeurs de q conduisant à une intensité lumineuse maximale ( franges brillantes). Les angles étant petits on peut confondre q, sin q et tanq. réponse :
- En déduire l'expression de la distance i ( appelée interfrange) séparant les centres des deux franges brillantes cons"cutives sur l'écran situé à une distance D= 4,90 m. Faire l'application numérique. réponse :
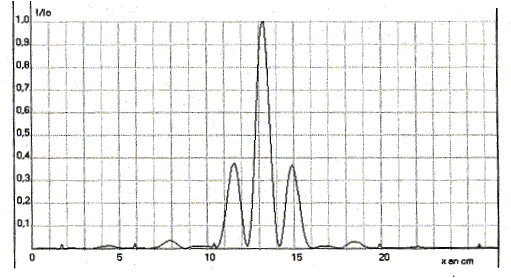
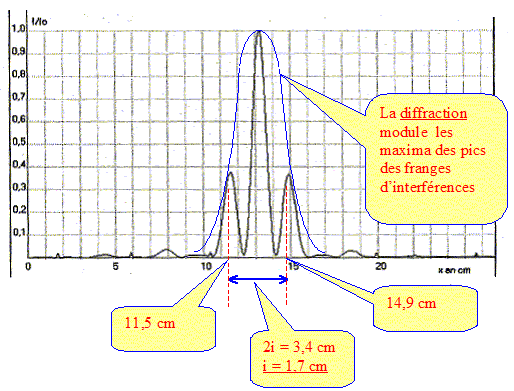
si k=0 : x=0 ( frange centrale brillante) si k = 1 : x= lD/a ( première frange brillante ) d'où i = x-0 = lD/a = 633 10-9*4,90 / 175 10-6 = 1,77 10-2 m = 1,77 cm. Un capteur optique disposé à la place de l'écran a permis d'obtenir la courbe suivante pour une distance D= 4,90 m.
x représente la position du capteur par rapport à une position décalée. Quel est l'interfrange ainsi mesuré ? Comparer avec la valeur théorique. Quel phénomène permet d'expliquer la diminution d'intensité des franges brillantes voisines de la frange centrale ?
Ne disposant pas d'un laser, on se propose de réaliser la même série d'expériences en remplaçant le laser par une lampe spectrale à vapeur de sodium émettant essentiellement deux raies de longueurs d'onde dans le vide 589,0 nm et 589,6 nm. On éclaire donc les deux fentes de Young à l'aide de la lampe spectrale disposée juste derrière le plan des fente, hélas on observe aucune frange sur l'écran. Ce phénomène peut être expliqué par une qualité particulière que possède le laser et que ne possède pas la lampe spectrale, laquelle ? Le laser est une source de lumière cohérente.
|
|
|
|