Aurélie 3/05/07
 

Concours kine Rennes : dispersion de la lumière ; 2007

En poursuivant votre navigation sur ce site, vous acceptez l’utilisation de Cookies vous proposant des publicités adaptés à vos centres d’intérêts.

. .
.
.

 

Dispersion de la lumière ( 5 pts)

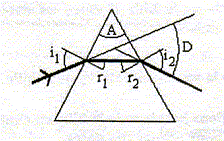
Un prisme de verre d'indice n, placé dans l'air, a pour section droite un triangle d'angle au sommet A=60°. La déviation d'un rayon monochromatique dans le prisme est repérée par l'angle de déviation D formé par le rayon incident pénétrant dans le prisme et par le rayon émergent sortant par la seconde face.

 

La déviation s'écrit : D = i1+i2-A avec A= r1+r2.

Deuxième loi de Descartes : lors du passage d'un milieu d'indice n1 à un milieu d'indice n2 : n1 sin i1 = n2 sin i2.

  1. Rappeler la définition d'un milieu dispersif et celle de l'indice de réfraction.
  2. L'idice de l'air étant égal à 1,000 et celui du verre étant noté n, écrire la deuxième loi de Descartes :
    - Au point M ( point de la face d'entrée du prisme où le rayon incident pénètre dans le prisme)
    - Au point P ( point de sortie du prisme où le rayon émergent sort du prisme)
  3. Un rayon lumineux provenant d'une lampe à vapeur métallique arrive sur la surface du prisme. Sa lumière se compose de deux radiations intenses de longueurs d'onde dans le vide respectives : l B=4680, nm et lR=635,5 nm.
    Les indices du prisme pour ces radiations sont nB=1,521 et nR=1,503.
    - Calculer la longueur d'onde dans le verre et la fréquence de ces deux radiations.
    - Déterminer les déviations DR et DB si l'angle d'incidence en M vaut 50,0°. En déduire la radiation la plus déviée.
Dispersion de la lumière :

 Définition d'un milieu dispersif et de l'indice de réfraction :

Dans un milieu dispersif, la célérité d'une onde dépend de sa fréquence.

L'indice de réfraction est égal au rapport de la célérité de la lumière dans le vide à la célérité de la lumière dans le milieu.

Deuxième loi de Descartes :
- Au point M ( point de la face d'entrée du prisme où le rayon incident pénètre dans le prisme)

Le milieu 1 est l'air d'indice nair = 1,000 ; le milieu 2 est le verre d'indice n.

sin i1 = n sin r1.
- Au point P ( point de sortie du prisme où le rayon émergent sort du prisme)

Le milieu 1 est le verre d'indice n ; le milieu 2 est l'air d'indice nair = 1,000.

n sin r2 = sin i2.

Un rayon lumineux provenant d'une lampe à vapeur métallique arrive sur la surface du prisme. Sa lumière se compose de deux radiations intenses de longueurs d'onde dans le vide respectives : l B=468,0 nm et lR=635,5 nm.
Les indices du prisme pour ces radiations sont nB=1,521 et nR=1,503.
Longueur d'onde dans le verre de ces deux radiations :

l 0 = c/f ; l = v/f ; l 0 /l =c/v = n d'où l =l 0 /n.

radiation bleue : l B/nB=468,0 / 1,521 =307,7 nm

radiation rouge : lR/nR=635,5 /1,503 =422,8 nm.

fréquence de ces radiations :

La fréquence ne dépend pas du milieu de propagation

fB= c/l B = 3,00 108 / 468 10-9 =6,41 1014 Hz.

fR= c/l R = 3,00 108 / 635,5 10-9 =4,72 1014 Hz.
Déviations DR et DB si l'angle d'incidence en M vaut 50,0° :
radiation bleue
radiation rouge
angle d'incidence en M
i1 = 50,0° ; sin 50,0 = 0,766
angle r1 ; sin r1 = 0,766 / n
0,766/1,521 =0,504 ; 30,24°
0,766 / 1,503 =0,510 ; 30,64°
angle r2 ; A-r1 = 60 -r1
60-30,24 =29,76°
60-30,64 = 29,36°
sin r1
sin 29,76 = 0,4963
sin 29,36 = 0,4903
angle i2 ; sin i2 =n sin r2
sin i2 =1,521*0,4963 =0,755 ; 49,0°
sin i2 =1,503*0,4903 =0,737 ; 47,5°
déviation : i1 +i2 -60
50+49,0-60 = 39,0°
50+47,5-60 =37,5°

La radiation bleue est la plus déviée.

 
 

retour -menu