Aurélie 054/06/07
 

concours orthoptie charge d'un condensateur. Montpellier 2006

En poursuivant votre navigation sur ce site, vous acceptez l’utilisation de Cookies vous proposant des publicités adaptés à vos centres d’intérêts.

. .
.
.

 

On réalise le circuit de la figure 1. Il comporte un générateur G, un condensateur, un ampèremètre et un interrupteur.

  1. A la date t=0, le condensateur étant préalablement déchargé, on ferme l’interrupteur. L’intensité indiquée par l’ampèremètre est constante et vaut I=12µA. Un dispositif non représenté sur la figure permet de relever la tension uc aux bornes du condensateur toutes les 0,5 s :
    t(s)
    0
    0,5
    1
    1,5
    2
    2,5
    3
    3,5
    4
    uc(V)
    0
    1,32
    2,64
    4,00
    5,35
    6,70
    7,98
    9,20
    10,6
    - Rappeler la relation entre la charge q du condensateur et l’intensité constante I du courant.
    - Calculer une valeur moyenne de la capacité C du condensateur à l’aide des valeurs du tableau.
    - On donne la courbe représentant les variations de la charge q en fonction de la tension uc (fig 2). En déduire une valeur approximative de la capacité C du condensateur.
 

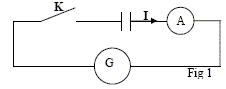
Relation entre la charge q du condensateur et l’intensité constante I du courant.

D'une part q= It ; d'autre part q= Cuc ;

Cuc = It ; uc = I/ C t ; uc = 1,2 10-5 / C t.


Valeur moyenne de la capacité C du condensateur à l’aide des valeurs du tableau  
t(s)
0
0,5
1
1,5
2
2,5
3
3,5
4
uc(V)
0
1,32
2,64
4,00
5,35
6,70
7,98
9,20
10,6
uc/t
xxxxx
2,64
2,64
2,67
2,67
2,68
2,66
2,63
2,65
valeur moyenne de uc/t : 2,65 V s-1.

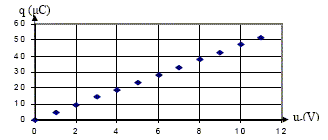
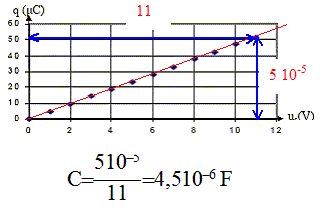
Par suite : 2,65 = 1,2 10-5 / C

d'où C= 1,2 10-5 / 2,65 = 4,5 10-6 F.

On donne la courbe représentant les variations de la charge q en fonction de la tension uc (fig 2).

Valeur approximative de la capacité C du condensateur.

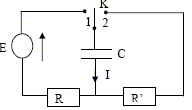
On réalise maintenant le montage de la figure 3 pour étudier la charge d’un condensateur à travers un conducteur ohmique. A t=0, le condensateur étant déchargé, on positionne l’interrupteur sur la position 1.

R=2,2 kW , R'=10 kW

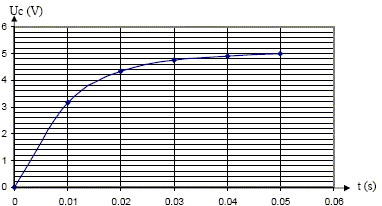
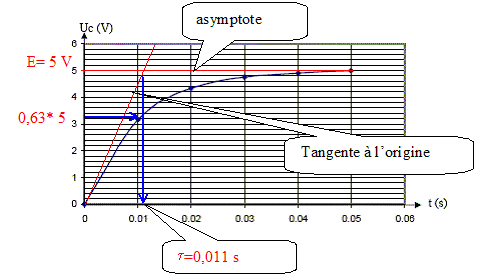
Equation différentielle E= RC duc/dt + uc vérifiée par la tension uc aux bornes du condensateur pendant la charge.

Additivité des tensions : E= uc+Ri

Or i = dq/dt et q = Cuc d'où : i = C duc/dt

E = uc+RC duc/dt. (1)

La solution de cette équation est de la forme uc=A(1-exp(-at)).

Identifions A et a en fonction de E, R et C.

duc/dt = Aa exp(-at)

repport dans (1) : E= A(1-exp(-at)) + RCAa exp(-at)

E= A+ A( RCa-1)exp(-at)

Cette égalité est vérifiée quelque soit t si A= E et si a= 1/(RC).

D'après le graphe de la figure 4, valeur de E.

-Définir la constante de temps t du circuit. Déterminer sa valeur d'après le graphe de la figure 4. En déduire une nouvelle valeur de C.

La constante de temps est égale au produit RC.

Si R=2,2 kW = 2200 W alors C= t/R = 0,011/2200 = 5 10-5 F.

Cette valeur et celles trouvées au 1) b) et au 1) c) sont elles compatibles avec la valeur indiquée par le fabricant : 4,7 µF à 10% près ?

Ecart relatif : (5-4,7 ) / 4,7*100 = 6,4%

Or l'indication du fabricant est à 10 % près.

Les valeurs trouvées sont compatibles avec la valeur du fabriquant.

 

- On place maintenant l'interrupteur en position 2. La décharge du condensateur est elle plus lente ou plus rapide que sa charge ?

La nouvelle constante de temps vaut t' = R'C avec R' > R. 

  donc t ' > t : la décharge sera plus lente que la charge.

 


retour -menu