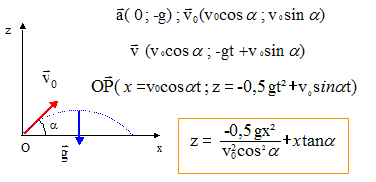Aurélie 04/06/07
 

concours orthoptie Projectile. Montpellier 2006

En poursuivant votre navigation sur ce site, vous acceptez l’utilisation de Cookies vous proposant des publicités adaptés à vos centres d’intérêts.

. .
.
.

 

Dans un référentiel terrestre considéré comme galiléen, on étudie la trajectoire d’un projectile assimilé à un point matériel. A un instant t=0 le projectile est lancé d’un point O, origine des coordonnées. Sa vitesse v0 fait un angle a avec l’axe x’Ox horizontal (fig 1). On néglige l’action de l’air et on note g l’accélération de la pesanteur avec g=9,81m.s-2.

 

  1. En appliquant la 2ème loi de Newton, établir les lois horaires x(t) et z(t) du mouvement du projectile en fonction de v0, g et a.
  2. En déduire l’équation de la trajectoire z=f(x) de la trajectoire du projectile.
  3. On veut atteindre un point A situé à une distance d de O, sur l’axe x’Ox (fig 1). En remarquant que l’altitude de A est nulle, exprimer sin(2a) en fonction de g, v0 et d.
    - Exprimer en fonction de g et d la valeur limite vl que doit dépasser v0 pour pouvoir atteindre le point A. Quelle est la valeur de     a lorsque v0= vl ?
    - Calculer     a pour d=50 m et v0=40 m/s. Quelle est l’altitude maximale atteinte dans ces conditions ?
  4. Calculer les abscisses des 2 points B et C d’altitude z=h qui peuvent être atteints si v0=30 m/s, a =25° et h=5 m (fig 2)

 

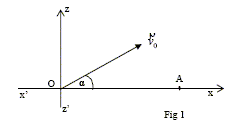
On veut atteindre un point A situé à une distance d de O, sur l’axe x’Ox (fig 1).

Expression de sin(2a) en fonction de g, v0 et d.

z=0 s'écrit : -0,5 g d2 / ( v0 cos a )2 + d sin a / cos a =0

Multiplier par cos a et diviser par d chaque terme.

-0,5 g d / ( v02 cos a ) + sin a =0

0,5 g d / ( v02 cos a )= sin a

gd = 2 v02 cos a sin a avec 2 cos a sin a = sin (2a)

sin (2a) = gd/ v02.


Expression en fonction de g et d la valeur limite vl que doit dépasser v0 pour pouvoir atteindre le point A.

d = v02sin (2a)/ g

La situation la plus favorable ( vitesse minimale) correspond a : sin (2a) = 1 soit a = 45°.

On trouve la valeur minimale de la vitesse en écrivant que sin (2a) = 1 d'où v2l = gd

vl = (gd)½.
Calcul de a pour d=50 m et v0=40 m/s :

d = v02sin (2a)/ g donne : sin (2a) = gd/v02= 9,81*50/402 =0,306

2a = 17,8 ° ; a = 8,9°.

Altitude maximale atteinte dans ces conditions :

Lorsque l'altitude maximale est atteinte, la vitesse est horizontale, c'est à dire que la composante verticale de la vitesse est nulle :

vz=-gt + v0 sin a =0 donne t = v0 sin a/g

Repport dans l'expression de z : zmax = -0,5 g( v0 sin a/g)2 + ( v0 sin a)2 / g

zmax = ( v0 sin a)2 / (2g)

zmax = ( 40*sin 8,9 )2 / (2*9,81) = 1,95 m.

 

 

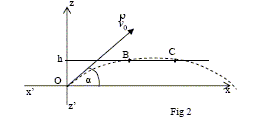
Abscisses des 2 points B et C d’altitude z=h qui peuvent être atteints si v0=30 m/s, a =25° et h=5 m (fig 2)

Ecrire que z= h : 5 = -0,5 *9,81 x2 / (40*cos25)2 + x tan 25.

-3,73 10-3 x2 +0,466 x-5=0

D = 0,2174 -7,46 10-2 = 0,1428 ; D½= 0,378.

xB= 11,8 m ; xC= 113 m.


retour -menu