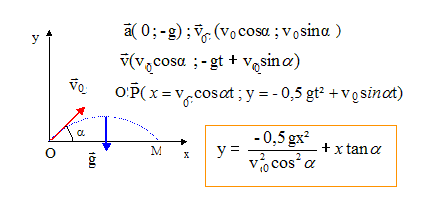Aurélie 15/05/07
 

concours orthoptie réflexion totale et fibre optique ; projectile et lanceur (ressort comprimé ). Nantes 2004

En poursuivant votre navigation sur ce site, vous acceptez l’utilisation de Cookies vous proposant des publicités adaptés à vos centres d’intérêts.

. .
.
.

réflexion totale et fibre optique : 

  1. Un rayon lumineux arrive sur un dioptre plan ( plan de séparation d'un milieu d'indice n1 avec un milieu d'indice n2< n1 ) avec une incidence i1.
    - Déterminer les caractéristiques du rayon réfléchi et réfracté ( un schéma est conseillé).
    - A quelle condition sur i1, seul le rayon réfléchi existe ?
    - Déterminer l'angle i1 limite pour n1 = 1,5 et n2 = 1,47.
  2. Etude d'une fibre optique à saut d'indice :
    - Le coeur de la fibre est constitué d'un milieu d'indice n1 = 1,5. La gaine a un indice n2=1,47. L'indice de l'air est noté nA=1. Tracer qualitativement le trajet du rayon arrivant en O, avec un angle     q par rapport à l'axe de la fibre.
    Si     q = q L, le rayon reste entièrement confiné dans la gaine. Justifier et calculer q L.
    - On émet à l'entrée de la fibre des impulsions lumineuses à une fréquence f. On admettra que l'angle     q peut prendre toutes les valeurs possibles entre q et q L. Déterminer le temps mis par le signal lumineux pour parcourir la fibre de longueur 10 m pour q =0 et q = q L.
    - A la sortie de la fibre on pourra distinguer les impulsions lumineuses si f <fmax. Calculer fmax.
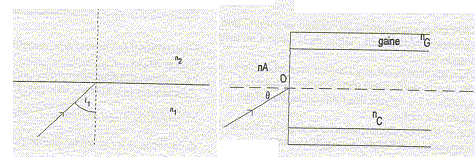
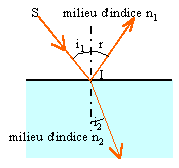
Lois de Descartes relatives à la réflexion et à la réfraction de la lumière :

Les trois rayons incident, réfléchi et réfracté sont dans le même plan ; l'angle d'incidence i1 est égal à l'angle de réflexion r. Les angles d'incidence i1 et réfracté i2 sont reliés par la relation : n1 sin i1 = n2 sin i2.

Condition sur i1, pour que seul le rayon réfléchi existe :

sin i2 = n1 /n2 sin i1 ; sin 90 = n1 /n2 sin i1 lim ; 1 = n1 /n2 sin i1 lim ; sin i1 lim = n2 /n1.

Si sin i1 est supérieur à n2 /n1 , il y a réflexion totale. ( le rayon réfracté n'existe pas )

sin i1 lim = 1,47/1,5 =0,98 ; i1 lim = 78,5°.


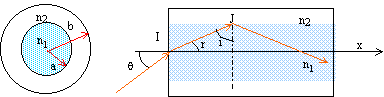
Le coeur de la fibre est constitué d'un milieu d'indice n1 = 1,5. La gaine a un indice n2=1,47. L'indice de l'air est noté nA=1.


Si q = q L, le rayon reste entièrement confiné dans la gaine.

Calcul de q L:

en I, dioptre air/coeur : nair sin q = n1 sin r ; sin q = n1 sin r (1)

en J, il y a réflexion totale : dioptre coeur/gaine : n1 sin i = n2 sin 90 = n2 ; sin i = n2 /n1 = 1,47 / 1,500 = 0,98 ; i = 78,5 °

Les angles i et r sont complémentaires soit sin r = cos i = cos 78,5 = 0,199

de plus (1) s'écrit : sin a = n1 sin r = 1,5*0,199 =0,298 ; q L= 17,4°.


On émet à l'entrée de la fibre des impulsions lumineuses à une fréquence f. On admettra que l'angle q peut prendre toutes les valeurs possibles entre q et q L. Temps mis par le signal lumineux pour parcourir la fibre de longueur 10 m pour q =0 et q = q L :

Figure ci-dessus, expression de IJ : ( on note h la projection de IJ sur l'axe de la fibre)

cos r = h/IJ; or sin q = n1 sin r ; cos² r + sin² r = 1 ;

h²/IJ² +( sin q / n1 )² = 1 ; h/IJ = [1-( sin q / n1 )² ]½.

Le rapport entre la longueur L de la fibre et le trajet d suivi par la lumière est : L/d =[1-( sin q / n1 )² ]½

d = L[1-( sin q / n1 )² ]-½.

pour q=0 , d0 =10 m ; pour qL =17,4 , d12 =10 [1-(sin17,4/1,5)²]-½=10,20 m

Célérité de la lumière dans le coeur : v = c/n1 = 3 108 / 1,5 = 2 108 m/s.

t0 =10 / 2 108 = 5 10-8 s ; tL =10,2 / 2 108 = 5,1 10-8 s ;
A la sortie de la fibre on pourra distinguer les impulsions lumineuses si f <fmax.

Calcul de fmax : 1/(tL-t0) = 109 Hz.

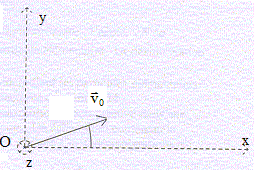
 Projectile et lanceur.

Un projectile de masse m est placé sur un ressort comprimé. On lâche le système sans vitesse initiale ; le projectile à la sortie du lanceur possède une vitesse v0. Le lanceur est placé au sol ; l'orientation du lanceur peut être modifiée. 

  1. A l'instant initial, x=0, y=0 et z=0 et le vecteur vitesse initiale est compris dans le plan Oxy et forme un angle a avec l'horizontale. Le champ de pesanteur a une intensité g. On néglige la force de frottement de l'air.
    - Déterminer l'évolution temporelle des coordonnées du vecteur vitesse puis l'évolution des coordonnées du projectile.
  2. Déterminer la valeur de a permettant d'obtenir l'altitude maximale. Exprimer cette altitude en fonction de g et v0.
  3. Déterminer la valeur de a permettant d'obtenir la portée maximale. Exprimer cette altitude en fonction de g et v0.

Etude du lanceur :

Le ressort possède une constante de raideur k, sa longueur à vide est OB et il est comprimé de a= AB avant le lancement. La vitesse atteinte par le projectile à la sortie du lanceur varie avec l'angle de lancement.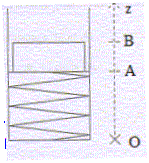

  1. Le lanceur est horizontal ( a=0), déterminer la vitesse à la sortie du lanceur en fonction de k, m, g et a dans l'hypothèse de l'absence de frottement.
  2. Le lanceur est vertical ( a=90°), déterminer la vitesse à la sortie du lanceur en fonction de k, m, g et a dans l'hypothèse de l'absence de frottement.
  3. A quelle conditions sur k, a, m et g peut-on considérer que la norme du vecteur vitesse à la sortie du lanceur, est indépendante de son orientation ?
 

Evolution temporelle des coordonnées du vecteur vitesse puis l'évolution des coordonnées du projectile :

Le mouvement est dans le plan défini par les vaecteurs vitesse initiale et accélération : z(t) = 0 ; v(t) = 0.

Valeur de a permettant d'obtenir l'altitude maximale :

A l'altitude maximale la composante verticale de la vitesse est nulle : 0 = -gt + v0 sina soit t = v0 sina /g.

Repport dans y(t) : ymax = -0,5 g(v0 sina /g)2 + (v0 sina )2 /g = ½ (v0 sina )2 /g.

Si a =90 °, l'altitude est maximale et vaut : v02 /(2g)

Valeur de a permettant d'obtenir la portée maximale :

yM=0 = -½gxM2 /(v0 cosa )2+ xM tana ;

d'où xM= 0 et xM = v02 sin (2a) /g.

La portée est maximale si a = 45 ° ; sa valeur est v02 /g.

Le lanceur est horizontal ( a=0) ; dans l'hypothèse de l'absence de frottement.

Vitesse à la sortie du lanceur en fonction de k, m et a :

L'énergie mécanique est initialement sous forme potentielle élastique : ½k a2.

L'énergie mécanique est sous forme cinétique au moment du départ du projectile : ½mv2.

L'énergie mécanique se conserve : ½k a2 = ½mv2.

v = (k/m)½a.

Le lanceur est vertical ( a=90°) ; dans l'hypothèse de l'absence de frottement.

Vitesse à la sortie du lanceur en fonction de k, m, g et a :

On choisit comme origine des énergies potentielles, le point E, position d'équilibre, longueur du ressort Léq.

Le projectile quitte le lanceur au moment où la tension du ressort est égale au poids ; la longueur du ressort est alors Léq :

mg = k( Léq -L0) ; Léq= L0+ mg/k. (1)

travail élémentaire résistant du poids parcours noté dx : - mg dx

en tenant compte de (1) : - mg dx = - k(Léq-L0)dx

travail élémentaire dW moteur de la tension parcours noté dx :

T = k(L-L0) = k(L-Léq +Léq-L0) = k(L-Léq) + k(Léq-L0)

dW= k(L-Léq)dx + k(Léq-L0)dx

On note (L-Léq) = x : dW= kxdx + k(Léq-L0)dx

somme des travaux élémentaires : - k(Léq-L0)dx + kxdx + k(Léq-L0)dx = kxdx

intégrer sur tout le parcours : W = ½kx2 = ½k(L-Léq)2.

Ecrire le théorème de l'énergie cinétique entre le point le plus bas A et E :

½k(L-Léq)2 = ½mv12 ; v1 = (L-Léq)[k/m]½.

Or Léq =L0+ mg/k ; L-Léq = L- L0- mg/k = a-mg/k

v1 = (a-mg/k)[k/m]½.

Conditions sur k, a, m et g afin que a norme du vecteur vitesse à la sortie du lanceur, soit indépendante de son orientation :

v2 = v12 ; k/m a2 =k/m (a-mg/k)2 d'où :

a = -a +mg/k ; a = mg/(2k).

La solution a= a-mg/k conduirait à m=0.

  
 

retour -menu