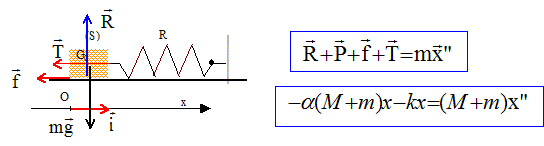Aurélie 02/04/07
 

Concours orthoptiste : pendule électrostatique, projectile, oscillateur mécanique 2004 ( Tours)

En poursuivant votre navigation sur ce site, vous acceptez l’utilisation de Cookies vous proposant des publicités adaptés à vos centres d’intérêts.

. .
.
.

 

Exercice 1 :

Deux petites boules ponctuelles sont suspendues au même point A par un fil de longueur L, de masse négligeable. Chaque boule possède une masse m et porte la charge électrique q. A l'équilibre les fils font un angle q avec la verticale.

  1. Exprimer la tension T d'un fil en fonction de L,q , sinq et k = 1/(4pe0).
  2. On place en A une charge électrique Q. Donner l'expression de Q pour que l'équilibre précédent soit conservé lorsqu'on coupe les fils.
 

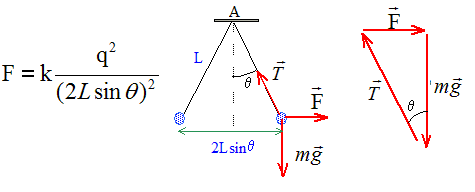
De plus sinq = F/T soit T= F / sin q ; T= kq2 / (4L2 sin3q).

On place en A une charge électrique Q. L'équilibre précédent est conservé lorsqu'on coupe les fils, si la force attractive, notée F1, exercée par Q sur q est égale à la tension. Les charges Q et q sont de signe contraire.

F1=kQq/ L2 ; T= kq2 /[(4L2 sin3q) ; kQq/ L2 = kq2 / [(4L2 sin3q) ; Q = q / (4 sin3q).

 

Exercice 2 :

Un projectile est envoyé avec une vitesse V0 dans une direction faisant un angle q avec le plan horizontal. L'engin qui tire le projectile se déplace sur ce plan à la vitesse v0.

  1. Comment doit être orienté le tube lançant le projectile pour que ce dernier parte à la verticale.
  2. Préciser la valeur de q lorsque V0 = 500 m/s et v0 = 15 m/s.
  3. Trouver la hauteur atteinte par le projectile.
Référentiel terrestre galiléen .
cosq = v0/V0 =15/500 = 0,03 ; q = 88,3°.

V= [ V0 2-v02]½ = [ 5002-152]½ = 499,77 m/s.
Hauteur atteinte par le projectile : H = V2/(2g) = [ 5002-152] / 19,6 =1,27 104 m.

Exercice 6 :

Une source ultrasonore S émet une vibration sinusoïdale à l'intérieur d'un tube contenant de l'eau. La fréquence émise par S est n0, la célérité de l'onde dans l'eau est V. La vibration issue de S provoque une variation de pression Y=Acos(w0t+j) en un point O tel que SO=l. Quelle est la variation de pression en un point M d'abscisse x>0 ?

--S------O-------M--------> x

Au point M, on observe la variation de pression produite en O avec un retard q=x/V :

Y=Acos[w0(t-x/V) +j].

Exercice 7 :

La masse de la terre est d'environ 5 1021 tonnes. Montrer que, si la terre avait été primitivement constituée uniquement de plutonium, celui-ci aurait complétement disparu en 48 000 siècles, durée très inférieure à l'âge de la terre. La période du plutonium est 240 siècles. Masse d'une mole de plutonium = 249 g.

48 000 siècles correspond à : 48000/240 = 200 périodes.

A chaque période, le nombre de noyaux initiaux ( donc la masse initiale ) de plutonium est divisée par deux.

Au bout de 200 périodes, la masse de plutonium restante est égale à la masse initiale divisée par 2200 soit par : 1,6 1060.

Exercice 8 :

Un paquet d'ions monovalents est accéléré à partir du repos par un champ électrique de 3 104 V/m sur une distance d=0,33 cm. A la sortie de ce champ, il parcourt 1 mm en 87 10-9 s.
- Déterminer la masse d'un de ces ions.
- Quel temps faudrait-il à un paquet de protons pour parcourir 1 mm à la sortie du champ électrique ?

Le poids des ions est négligeable devant la force électrique de valeur F=eE.

La seconde loi de newton donne l'accélération a = eE/m ;

La vitesse des ions à la sortie du champ électrique vaut v2 = 2ad = 2eEd/m.

m = 2eEd/v2.

A la sortie de ce champ le mouvement est rectiligne uniforme : vitesse v = 10-3/87 10-9=1,15 104 m/s

m= 2*1,6 10-19 * 3 104 *3,3 10-4/(1,15 104 )2=2,4 10-26 kg.

Temps mis par un paquet de protons pour parcourir 1 mm à la sortie du champ électrique :

v2 = 2eEd/m= 2*1,6 10-19 * 3 104 *3,3 10-4 / 1,67 10-27 = 1,89 109 ; v = 4,36 104 m/s

Dt = 10-3 / 4,36 104 =2,3 10-8 s.
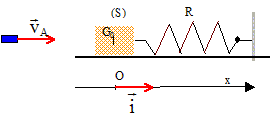
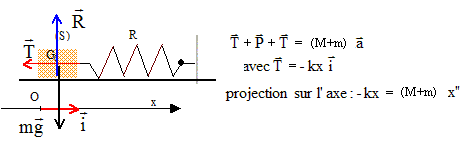
Exercice 3 :
Un bloc de bois B de masse M, est placé sur un plan horizontal. Un projectile A, de masse m, ayant une vitesse vA horizontale, frappe ce bloc et s'y encastre. Un ressort limite le déplacement de B. Avant le choc le ressort n'a aucune déformation. Après le choc, l'ensemble A+B se déplace en comprimant le ressort dans la direction Ox. Le coefficient de raideur du ressort est k.

  1. Le plan n'exerçant aucun frottement, calculer la vitesse aquise par l'ensemble A+B juste après le choc.
  2. Quel est en fonction du temps, le déplacement x du système A+B glissant sans frottement sur le plan ? Calculer la fréquence, la période, l'amplitude du mouvement.
  3. On suppose que le plan exerce une force de frottement horizontale sur le système glissant, opposée au mouvement. L'intensité de cette force est proportionnelle au déplacement x et à la masse m du mobile f=amx. Quel est alors le déplacement maximum de l'ensemble A+B après impact du projectile ?
    A.N : M=610 g ; m=30 g ; k=1,4 104 S.I ;     a= 6,55 104 S.I ; vA= 640 m/s.
Vitesse V aquise par l'ensemble A+B juste après le choc :  

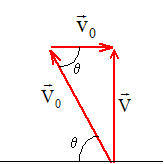
La conservation de la quantité de mouvement s'écrit : mvA = (M+m)V soit V= m/(M+m) vA = 0,03/0,64*640 = 30 m/s.

x"+k/(M+m) x=0 ; x"+w02x=0 avec w0 =[ k/(M+m)]½ =[1,4 104 / (0,61+0,03)]½ =148 rad/s

fréquence : f = w0/ (2p) = 148 / (6,28) = 23,55 Hz ; période T=1/f = 4,2 10-2 s.

Conservation de l'énergie mécanique : ½(M+m)V2 = ½kA2 ;

A= V[(M+m)/k]½ =30*[0,64/1,4 104]½ =0,20 m.

Déplacement x du système A+B : x(t) = 0,2 sin(148 t ).

On suppose que le plan exerce une force de frottement horizontale sur le système glissant, opposée au mouvement.

 Dans l'expression de l'amplitude il suffit de remplacer k par k1 = k+a(M+m) = (1,4 + 6,55*0,64)104 = 5,59 104 S.I

 Nouvelle amplitude A1 = V[(M+m)/k1]½ =30*[0,64/5,59 104]½ =0,10 m.

 Autre méthode : appliquer le théorème de l'énergie cinétique.

travail résistant de la tension -½kA12 ;  

travail résistant des frottements : -½a(M+m)A12 ;

variation de l'énergie cinétique : 0-½(M+m) V2.
 

retour -menu