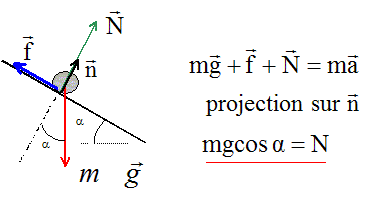|
Concours Kiné : mécanique, chute libre, frottement sur un plan incliné 2007 ( Nantes) En poursuivant votre navigation sur ce site, vous acceptez l’utilisation de Cookies vous proposant des publicités adaptés à vos centres d’intérêts. |
|
| .
. |
|
|
|
|
Exercice 2 :
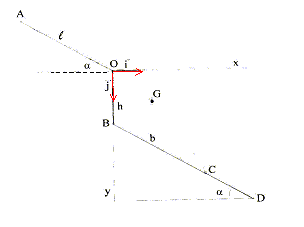
a=30° ; h= 20 m ; g = 10 m/s². On étudie le mouvement d'un solide S assimilé à un point matériel G de masse m. On considère que tous les mouvements se font sans frottement. Lâché de A sans vitesse initiale, le solide glisse sur le plan incliné AO et arrive en O avec une vitesse v0, puis effectue un mouvement aérien dans le plan de pesanteur et chute sur le plan incliné BD en un point C.
En fait la chute se fait en C' tel que BC' = b' = r b. On admet que cela est du aux frottements de S sur le plan incliné AO ; le mouvement aérien est toujours sans frottement. m = f/N avec f composante tangentielle ( force de frotement) de la réaction R su support ; N composante normale de la réaction du support.
On note L=AO, la distance parcourue sur le plan incliné. Expression de v0 en fonction de L, a et g : théorème de
l'énergie cinétique entre A et O :
DEc=½mv20-0 ½mv20 =mgLsin a : v20 =2gLsin a : v0 =[2gLsin a]½ =[2*10*40*sin30]½ =20 m/s. Le mouvement aérien est
étudié dans le repère (O, i, j). accélération : (0 ; g) ; vitesse initiale :(v0cosa ; v0 sin a ) La vitesse est une primitive de l'accélération : vx= v0cosa ; vy= gt +v0 sin a La position est une primitive de la vitesse : x = v0cosa t ; y = ½gt2+v0 sin a t t=
x/(v0cosa
; y =
½gx2/(v0cosa)2
+ x tan a y= a x+b avec a = tan a et b= h y = tan a
x
+h. yC = ½gxC2/(v0cosa)2 + xC tan a = tan a xC +h. ½gxC2/(v0cosa)2 = h ; xC2 =2h /g (v0cosa)2 ; xC =[2h /g]½v0cosa. Expression de b=BC en fonction de h, g et v0: yC -h = tan a xC = [2h /g]½v0sina. b2 = xC2 +(yC -h)2 =2h /g (v0cosa)2 + 2h /g (v0sina)2 =2h /gv20 b = [2h /g]½v0 ; b =(2*20/10)½*20 ; b=40 m. En fait la chute se fait en C' tel que BC' = b' = r b. On admet que cela est du aux frottements de S sur le plan incliné AO ; le mouvement aérien est toujours sans frottement. m = f/N avec f composante tangentielle ( force de frotement) de la réaction R su support ; N composante normale de la réaction du support. Montrons que la vitesse d'arrivée de S en O est v'0 = rv0. b' = r b =r [2h /g]½v0 ; d'autre part b'= [2h /g]½v'0 ; d'où v'0 = rv0.
Expression de m en fonction de r et a :
théorème de
l'énergie cinétique entre A et O :
DEc=½mv'20-0 Travail résistant de f : -fL ; N perpendiculaire au plan ne travaille pas. ½mv'20 =mgLsin a -fL ; or ½mv20 =mgLsin a d'où : ½mv'20 =½mv20 -fL ; or v'0 = rv0. d'où : ½m r2v20 =½mv20 -fL ; fL= ½mv20(1-r2) or v20 =2gLsin a d'où : f = mgsin a(1-r2) m= f/N = mgsin a(1-r2) / (mg cosa) ; m = (1-r2)tan a. Calcul de m si r = 0,90 : m = (1-r2)tan a = (1-0,92) tan30 ; m =0,11.
|
|
|
|
|
|
|