|
Concours Kiné : charge d'un condensateur ; dipôle RLC 2007 ( Nantes) En poursuivant votre navigation sur ce site, vous acceptez l’utilisation de Cookies vous proposant des publicités adaptés à vos centres d’intérêts. |
|||||||
| .
. |
|||||||
|
|||||||
|
Exercice 1 :
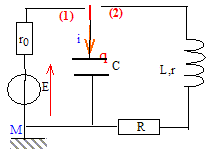
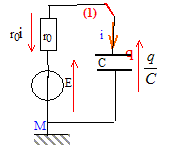
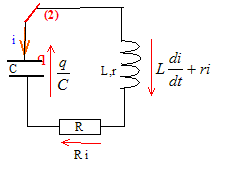
Le générateur a une fem E= 6,00 V et une résistance interne r0 = 100 W ; C= 10,0 mF ; L= 1,01 H ; R résistance ajustable. Le condensateur étant déchargé, on connecte à l'instant t=0 sur la position 1.
E-r0dq/dt =q/C dq/dt
+q/(r0C)=E/r0.
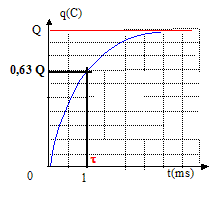
(1) Charge finale Q du condensateur : l'intensité est nulle en fin de charge ; la tension aux bornes du condensateur chargé vaut E. Q=CE ; Q= 10-5*6 = 6,00 10-5 C. Expression de la constante de temps t : q(t) = Q(1-exp (-t/t)) est solution de l'équation différentielle précédente ; dq/dt = Q/t exp (-t/t) repport dans (1) : Q/t exp (-t/t)+Q/(r0C) (1-exp (-t/t)) = E/r0. Cette relation est vérifiée quel que soit t si : Q/t =Q/(r0C) soit t =r0C. t =100*10-5 = 1,00 10-3 s. Courbe donnant q en fonction du
temps :
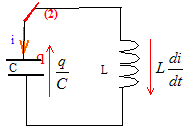
On ajuste R à 0 et on suppose r=0. Equation différentielle relative à la charge q du condensateur : R = 0 ; r=0.
Expression de la période T0 : q(t)=Q cos (2pt/T0) ; w0 =2p/T0 ; T0 =2p/ w0 T0 =2p (LC)½ =6,28(1,01 10-5)½ =20,0 10-3 s. En réalité r n'est
pas nulle et on a ajusté R à 350
W. Ld2q/dt2+(r+R)dq/dt+q/C=0 d2q/dt2
+(r+R)/L dq/dt + q/(LC)=0 cette équation
compte un terme d'amortissement
:(r+R)/L dq/dt
Résistance r de la bobine : T= T0 ( 1-e2)-½ avec e = ½RT(C/L)½. T2= T20 ( 1-e2)-1 ;(T0/T)2 =1-e2 ; e2 = 1-(T0/T)2 ; e = [1-(T0/T)2 ]½. de plus e = ½RT(C/L)½ d'où : ½RT(C/L)½= [1-(T0/T)2 ]½. RT = 2[(1-(T0/T)2) L/C]½. RT = 2[(1-(20/25)2)*1,01/10-5]½ =381 W ; r=RT-R=381-350=31 W. Le régime critique est obtenu quand T tend vers l'infini. Valeur RC de R pour obtenir le régime critique : Quand T tend vers l'infini e tend vers 1. 1= ½RT(C/L)½ ; RT=2(L/C)½ =2(1,01/10-5)½ = 636 W ; R=RT-r=636-31=605 W.
|
|||||||
|
|
|||||||
|
|