concours électroradiologie médicale cuivre et dibrome ; électrolyse. Nantes 2006

En poursuivant votre navigation sur ce site, vous acceptez l’utilisation de Cookies vous proposant des publicités adaptés à vos centres d’intérêts.

A. Réaction entre cuivre et dibrome.

On verse 250 mL d'une solution de dibrome de concentration égale à 0,10 mol/L dans un becher. On y ajoute 3,2 g de cuivre en poudre. On agite. On constate que la solution change de couleur : elle passe du jaune orangée, au vert, puis au bleu, tandis que le cuivre disparaît. On interprète cette transformation par la réaction dont l'équation est :

Cu(s) + Br₂(aq) = Cu²⁺(aq) + 2Br^-(aq) K= 1,25 10²⁵.

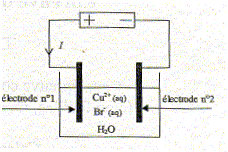
On réalise le montage ci-dessous :

L'intensité est constante I= 2,4 A ; les deux électrodes de graphite sont chimiquement inertes ; elles plongent dans 1 L de solution de bromure de cuivre CuBr₂ de concentration en soluté apporté c= 0,10 mol/L.

On met en évidence un dépot de cuivre sur l'une des électrodes et la formation de dibrome au niveau de l'autre électrode.

A. Réaction entre cuivre et dibrome.

On verse 250 mL d'une solution de dibrome de concentration égale à 0,10 mol/L dans un becher. On y ajoute 3,2 g de cuivre en poudre. On agite. On constate que la solution change de couleur : elle passe du jaune orangée, au vert, puis au bleu, tandis que le cuivre disparaît. On interprète cette transformation par la réaction dont l'équation est :

Cu(s) + Br₂(aq) = Cu²⁺(aq) + 2Br^-(aq) K= 1,25 10²⁵.

Demi-équations d'oxydoréduction pour les deux couples qui interviennent dans cette réaction.

Oxydation du cuivre : Cu(s) = Cu²⁺(aq) + 2e^-.

Réduction du dibrome : Br₂(aq) + 2e^- = 2Br^-(aq)

Le dibrome disparaît ( la teinte orangée va donc s'atténuer) ; des ions cuivre (II) apparaissent : une teinte bleue va progressivement apparaître.

Les ions bromures sont incolores.

Expression du quotient initial de réaction Q _{r i} :

Q _{r i} = [Cu²⁺(aq)] _i [Br^-(aq)] _i ² / [Br₂(aq)] _i

Ce quotient est nul car initialement [Cu²⁺(aq)] _i =[Br^-(aq)] _i =0

Le changement de couleur indique une évolution du système dans le sens direct.

De plus Q _{r i} <K : le critère d'évolution indique ce même sens d'évolution.

avancement maximal :

n(Cu) _i = m/M(Cu) = 3,2 / 63,5 =0,050 mol ; n(Br₂)_i=c V =0,25*0,1 =0,025 mol.

	avancement (mol)	Cu(s)	+ Br2(aq)	=Cu2+(aq)	+ 2Br-(aq)
départ	0	0,05	0,025	0	0
en cours	x	0,05-x	0,025-x	x	2x
fin	xmax	0,05-xmax	0,025-xmax	xmax	2xmax

Si Cu(s) est en défaut : 0,05-x_max =0 soit x_max =0,05 mol

Si Br₂(aq) est en défaut, 0,025-x_max=0 soit x_max =0,025 mol

Retenir la plus petite valeur.

Dans l'état final d'équilibre Q _r est égal à la constante d'équilibre : Q _{r éq} = K = 1,25 10²⁵.

Des calculs, lors de l'analyse de la solution finale, montre que x_éq = 0,025 mol.
La transformation est rapide :" On agite. On constate que la solution change de couleur"

totale : x_éq = x_max, le taux d'avancement final t =x_éq / x_max vaut 1.

spontanée : elle ne nécessite pas d'apport d'énergie extérieur.

B. Electrolyse d'une solution de bromure de cuivre.

On réalise le montage ci-dessous :

L'anode est reliée à la borne positive du générateur ( électrode n°1)

Oxydation de Br^- (aq) : 2Br^- (aq) = Br₂ (aq) + 2e^-.

La cathode est reliée à la borne négative du générateur ( électrode n° 2)

Réduction de Cu²⁺(aq) : Cu²⁺(aq) +2e^- = Cu(s)

Equation de la réaction d'électrolyse :

2Br^- (aq) + Cu²⁺(aq) = Cu(s) + Br₂(aq)

Expression de la constante d'équilibre K' :

K' =[ Br₂(aq)]_éq /([Cu²⁺(aq)]_éq[Br^- (aq)]_éq²) = 1/K = 1/1,25 10²⁵ = 8 10^-26.

Au bout de 5 min on obtient les concentrations suivantes en solution: [Br₂(aq)]=4 10^-3 mol/L ; [Cu²⁺(aq)]= 1,0 10^-1 mol/L ; [Br^-(aq)]=0,20 mol/L.
Expression du quotient de réaction Q'_r à cet instant :

Q'_r =[ Br₂(aq)] /([Cu²⁺(aq)][Br^- (aq)]²)

Q'_r =4 10^-3 / (0,1*0,2²)=1

Au cours de l'électrolyse , [ Br₂(aq)] augmente, [Cu²⁺(aq)] et [Br^- (aq)] diminuent : Q'_r = tend vers K.

La transformation est forcée : elle nécessite un apport d'énergie extérieur, sous forme d'énergie électrique.