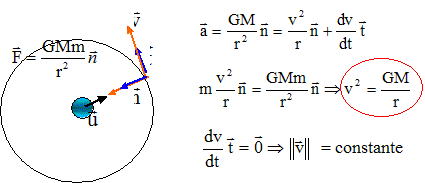Aurélie 21/05/07
 

concours Geipi satellites, supercondensateur : dipole RC et générateur de courant 2007

En poursuivant votre navigation sur ce site, vous acceptez l’utilisation de Cookies vous proposant des publicités adaptés à vos centres d’intérêts.

. .
.
.

exercice 3 : 

Les vecteurs sont écrits en gras et en bleu.

Au cours d’observations astronomiques, une planète P a été découverte hors du système solaire. Autour de cette planète gravite un satellite S qui décrit un mouvement circulaire uniforme de rayon r = 212 103 km. La période de révolution de S autour de P est de T = 296 heures. La masse du satellite S est notée m , sa vitesse est notée v. La masse de P est notée M.

On rappelle la valeur de la constante de gravitation universelle : G=6,6710-11m3.kg-1.s-2

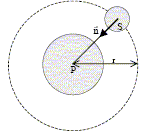
n est le vecteur unitaire orienté du centre de S vers le centre de P.

  1. Exprimer l’accélération a de S en fonction de v, r et n.
  2. Exprimer la force F P/S exercée par P sur S en fonction de m, M, G, r et n.
  3. Donner l’équation reliant v à r, G et M.
  4. Exprimer T2 en fonction de r, G et m.
  5. Donner les valeurs littérales et numériques de M.
    Afin que la vie puisse se développer à sa surface, la masse d’une planète doit être suffisante pour que la gravité soit en mesure de retenir des éléments relativement légers comme le carbone ou l'oxygène. Cependant, elle ne doit pas être trop grande sinon l’hydrogène est piégé, ce qui constitue un environnement chimiquement réducteur que les biologistes considèrent comme impropre à la vie. A titre d’exemple : la masse de Mercure vaut : 3,3.1023 kg , la masse de la Terre vaut : 6,0.1024 kg et la masse de Jupiter vaut : 1,9.1027 kg.
  6. La masse de la planète P semble-t-elle compatible avec l’apparition de la vie à sa surface ?
    La masse de l’étoile E autour de laquelle gravite P constitue également un paramètre décisif pour l’apparition et le développement de la vie sur P : A une étoile trop petite correspond une luminosité trop faible et donc un apport d’énergie insuffisant. En outre, la durée de vie d’une étoile diminue avec sa taille. Or il a fallu un milliard d’années pour que la vie apparaisse sur terre. On considère parfois que l’étoile doit avoir sa masse comprise entre 0,5 et 2 fois la masse du Soleil (msoleil=2,0.1030 kg).
  7. Sachant que la trajectoire de P autour de E est circulaire uniforme (Rayon r1=188.106 km, période T1=2440 heures), donner les valeurs littérales et numériques de mE, masse de l’étoile E.
  8. La masse de la planète E semble-t-elle compatible avec l’apparition de la vie sur P ?
Accélération a de S en fonction de v, r et n.

L'accélération est centripète : a = v2/r n.

Force F P/S exercée par P sur S en fonction de m, M, G, r et n.

La force est centripète : F P/S = GM m /r2n.

Equation reliant v à r, G et M : v= [GM/r]½.

Expression de T2 en fonction de r, G et m.

Le satellite décrit une circonférence 2pr en une période T à la vitesse v :

2pr = v T soit T = 2pr / v ; T2 = 4p2r2 / v2

remplacer v2 par son expression GM/r d'où : T2 = 4p2r3 /(GM). (3ème loi de Kepler )

Valeurs littérale et numérique de M :

M= 4p2r3 / (GT2) ; r = 2,12 108 m ; T = 296*3600 = 1,065 106 s.

M = 4*3,142 * (2,12 108 )3 / (6,67 10-11*1,0652 1012 )=4,97 1024 kg.


Afin que la vie puisse se développer à sa surface, la masse d’une planète doit être suffisante pour que la gravité soit en mesure de retenir des éléments relativement légers comme le carbone ou l'oxygène. Cependant, elle ne doit pas être trop grande sinon l’hydrogène est piégé, ce qui constitue un environnement chimiquement réducteur que les biologistes considèrent comme impropre à la vie. A titre d’exemple : la masse de Mercure vaut : 3,3.1023 kg , la masse de la Terre vaut : 6,0.1024 kg et la masse de Jupiter vaut : 1,9.1027 kg.

La masse de la planète P semble compatible avec l’apparition de la vie à sa surface car sa masse est du même ordre que celle de la terre.
La masse de l’étoile E autour de laquelle gravite P constitue également un paramètre décisif pour l’apparition et le développement de la vie sur P : A une étoile trop petite correspond une luminosité trop faible et donc un apport d’énergie insuffisant. En outre, la durée de vie d’une étoile diminue avec sa taille. Or il a fallu un milliard d’années pour que la vie apparaisse sur terre. On considère parfois que l’étoile doit avoir sa masse comprise entre 0,5 et 2 fois la masse du Soleil (msoleil=2,0.1030 kg).

La trajectoire de P autour de E est circulaire uniforme (Rayon r1=188.106 km, période T1=2440 heures) :

Valeurs littérales et numériques de ME, masse de l’étoile E.

T12 = 4p2r13 /(GME). (3ème loi de Kepler )

ME= 4p2r13 / (GT12) ; r1 = 1,88 1011 m ; T1 = 2440*3600 = 8,784 106 s.

M = 4*3,142 * (1,88 1011 )3 / (6,67 10-11*8,7842 1012 )=5,1 1031 kg.

La masse de la planète E ne semble pas compatible avec l’apparition de la vie sur P : la masse de l'étoile est voisine de 25 fois la masse du soleil.

"l’étoile doit avoir sa masse comprise entre 0,5 et 2 fois la masse du Soleil "
Exercice 4 :

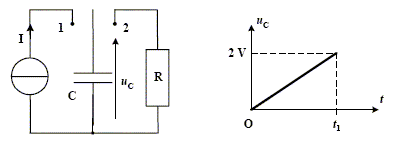
Dans le problème suivant, on utilise un supercondensateur de capacité élevée C = 1800 F.

Ce condensateur de 400 g a un diamètre de 50 mm et une hauteur de 150 mm.

A l’instant t = 0, on place l’interrupteur en position 1. On charge alors ce condensateur à l’aide d’un générateur de courant qui permet de délivrer une intensité constante I = 100 A. On obtient la courbe de charge ci-dessous.

 

 

  1. À quel instant t1 la tension aux bornes du condensateur atteint U1=2V ?
  2. Quelle est l’énergie Ec1 emmagasinée par ce condensateur à cet instant t1 ?
    A l’instant t = t1, on place l’interrupteur en position 2. On décharge ce condensateur à travers une résistance R = 2 W jusqu’à l’instant t2 où uC(t2) = U2= 1,5 V.
    L’équation donnant la tension aux bornes du condensateur durant cette décharge est : uC = A + B exp (-(t-t1) / t).
  3. Déterminer A, B et t.
  4. A quel instant t2 la tension aux bornes du condensateur atteint U2=1,5 V ?
  5. En supposant que la décharge du condensateur se passe sans pertes d’énergie, quelle est l’énergie ER dissipée par effet Joule dans la résistance R entre t1 et t2 ?
    En déduire la puissance moyenne PR dissipée par effet Joule dans la résistance R entre t1 et t2.
    On définit le rendement comme le rapport entre l’énergie restituée lors de la décharge et l’énergie emmagasinée lors de la charge. Les accumulateurs traditionnels du type batterie de voiture ont un rendement de l’ordre de 50 %. On mesure la puissance moyenne dissipée par R entre t1 et t2. On obtient 1,4 Watt.

Calculer le rendement h de ce supercondensateur. Comparer et conclure.  

 

Instant t1 où la tension aux bornes du condensateur atteint U1=2V :

Expression de la charge d'une armature : Q= It et Q= CuC.

It =CuC ; t = C/I uC.

t1 = 1800/100*2 = 36 s.

Energie Ec1 emmagasinée par ce condensateur à cet instant t1 :

Ec1 =½CuC2 = 0,5*1800*4 = 3,6 103 J.
A l’instant t = t1, on place l’interrupteur en position 2. On décharge ce condensateur à travers une résistance R = 2 W jusqu’à l’instant t2 où uC(t2) = U2= 1,5 V.
L’équation donnant la tension aux bornes du condensateur durant cette décharge est : uC = A + B exp (-(t-t1) / t).

Détermination de A, B et t :

A l'instant t = t1, uC=2 V : 2=A+B.

Quand t tend vers l'infini, le condensateur est déchargé : uC=0 : 0 = A ; B=2.

t= RC = 2*1800 ; t= 3600 s.

Instant t2 où la tension aux bornes du condensateur atteint U2=1,5 V :

ln(uC/2) =-(t2-t1) / t ; t ln(2/uC) =t2-t1 ; t2=t1+ t ln(2/uC)

t2=36+ 3600 ln(2/1,5) ; t2= 1,07 103 s.

En supposant que la décharge du condensateur se passe sans pertes d’énergie, l’énergie ER dissipée par effet Joule dans la résistance R entre t1 et t2 vaut :

énergie finale stockée - énergie initiale stockée = ½C ( 22-1,52)

ER = 900 (4-2,25) ; ER = 1,57 103 J
Puissance moyenne PR dissipée par effet Joule dans la résistance R entre t1 et t2 :

PR = ER /(t2-t1) = 1,57 103 / (1070-36) ; PR = 1,52 W.


On définit le rendement comme le rapport entre l’énergie restituée lors de la décharge et l’énergie emmagasinée lors de la charge. Les accumulateurs traditionnels du type batterie de voiture ont un rendement de l’ordre de 50 %. On mesure la puissance moyenne dissipée par R entre t1 et t2. On obtient 1,4 Watt.

Rendement h de ce supercondensateur :

h = 1,4/1,52*100 ; h = 92 %, valeur bien supérieure au rendement d'un accumulateur.
 

retour -menu