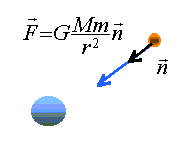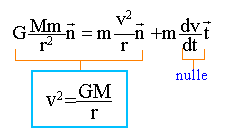Aurélie 10/05/07
 

concours ergo Berck satellite ; oscillateur mécanique ; poussée d'Archimède ; vitesse limite de chute. 2007

En poursuivant votre navigation sur ce site, vous acceptez l’utilisation de Cookies vous proposant des publicités adaptés à vos centres d’intérêts.

. .
.
.

 

On considère un satellite de masse m en orbite autour de la terre. Le satellite évolue à une altitude h par rapport à la surface de la terre. On se place dans le référentiel géocentrique.

Parmi les affirmations suivantes, combien il y en a t-il d'exactes ?

- La constante de gravitation universelle vaut G= 6,67 10-11 N kg2 m-2. Faux.

F= G M m / (R+h)2 soit G = F(R+h)2/(M m)

l'unité est donc N m2 kg-2.

- La force de gravitation exercée par la terre sur le satellite est inversement proportionnelle au carré de l'altitude h.Faux.

"inversement proportionnelle au carré de la distance" ; la distance du centre de la terre au satellite vaut : ( R+h)2.

- Le mouvement du centre d'inertie du satellite est uniforme. Exact.

uniforme signifie " la valeur de la vitesse reste constante"

- L'accélération du centre d'inertie du satellite est nulle. Faux.

Accélération centripète ( dirigée vers le centre de la terre) de valeur v2/(R+h).

- La valeur de la vitesse du centre d'inertie du satellite dépend de la masse du satellite. Faux.

Un ressort à spires non jointives, de masse négligeable et de constante de raideur k est suspendu à un support vertical par l'une de ses extrémités. Un solide S de masse m est accroché à l'autre extrémité du ressort. Le ressort s'allonge de x0 = 10 cm : c'est la position d'équilibre.

A partir de cette position d'équilibre, le solide est tiré vers le bas suivant la verticale, puis lâché sans vitesse initiale.

Le solide effectue des oscillations non amorties autour de la position d'équilibre. ( g = 10 N/s²)

Calculer la période ( en s) des oscillations du système. ( 0,23 ; 0,34 ; 0,48 ; 0,52 ; 0,63; aucune réponse exacte)

T = 2p [m/k]½ ;

A la position d'équilibre le poids compense la tension du ressort : mg = k x0.

d'où m / k = x0 / g = 0,10 / 10 ; m / k = 0,01 s2 ; [m/k]½ = 0,1 s.

T = 6,28 *0,1 = 0,63 s.

 

Un cube de bois de côté a = 20 cm flotte dans de l'eau. Le cube émerge d'une hauteur h par rapport à la surface de l'eau.

masse volumique du bois rB=850 kg m-3.

masse volumique de l'eau rE=100 kg m-3.

Calculer h ( en cm). ( 3,0 ; 6,0 ; 12,0 ; 17,0 ; 20,0 ; aucune réponse exacte).

volume du bois : a3 ; masse du bois : rBa3 ; poids du bois : rBa3 g.

volume immergé : a2(a-h) ; poussée = a2(a-h)rE g.

rBa3 g =a2(a-h)rE g ; rBa = (a-h)rE ;

rBa /rE = a-h ; h = a(1-rB /rE ) ; h = 20(1-0,85) = 20*0,15 = 3,0 cm.

Une bille de masse m= 64 g est en chute verticale dans l'air. On négligera la poussée d'Archimède exercée par l'air sur la bille.

L'air exerce sur la bille une force de frottement dont la valeur est de la forme f= kv2 avec k = 4,0 10-4 S.I et v la vitesse de la bille.

La bille atteint au bout d'un certain temps une vitesse limite. ( g = 10 N/kg)

Calculer la vitesse limite ( m/s) atteinte par la bille. ( 10 ; 20 ; 30 ; 40 ; 50 ; aucune réponse exacte)

La bille est soumise à son poids ( valeur mg) et à la force de frootement.

Lorsque la vitesse limite est atteinte, les deux forces se neutralisent ; elles ont même valeur.

mg = kvlim2 ; vlim2 = mg/k ; vlim =[ mg/k ]½ ;

vlim = [ 0,064*10 / 4 10-4 ]½ = [ 0,64 / 4 10-4 ]½ = [ 6400/ 4 ]½ = [ 1600 ]½ ; vlim = 40 m/s.

 
 

retour -menu