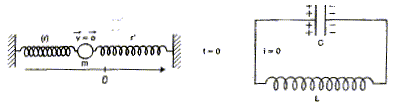|
Question
3 : 6 pts/20 sans
calculatrice
La figure ci dessous représente l'état de
chacun des deux oscillateurs à l'instant
t=0.
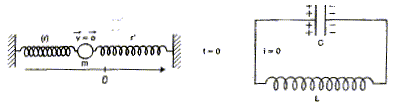
La masse m a une vitesse nulle
à l'abscisse x=-Xmax ; le ressort (r) est
comprimé au maximum ; le ressort r' est
étiré au maximum. Corrélativement le
condensateur possède la charge maximale
+qmax sur une face et -qmax sur
l'autre face, le courant étant nul.
L'oscillateur mécanique est
constitué de deux ressorts identiques ( même
longueur à vide et même constante de raideur k
). Soit O la position d'équilibre de cet oscillateur.
Ce point constitue aussi pour chacun des ressorts, la
position à vide. Ce point O sera pris comme origine
des abscisses.
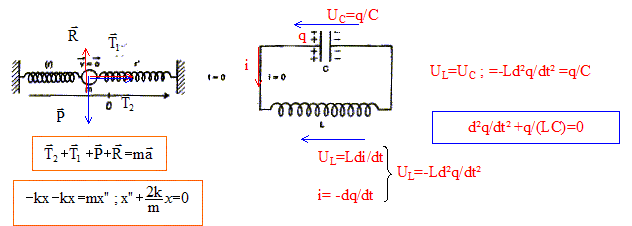
- Etablir l'équation
différentielle à laquelle satisfait
l'abscisse x(t) de la masse m pour le système
mécanique, et la charge q(t) du condensateur pour
le système électrique.
- En utilisant les conditions initiales, établir
les expressions de x(t) et de q(t).
- Etablir pour chaque système la période
propre T0 des oscillations.
- Reprendre la comparaison des
deux systèmes à la date t=0 et continuer la
comparaison en dessinant autant de doubles schémas
qu'il vous semblera nécessaire pour couvrir une
période entière. Indiquer sous chaque
schéma sous quelle forme se trouve
l'énergie et sa localisation.
|
x(t) = Xm cos( w0t+
j) avec w0=[2k/m]½.
|
q(t) = qmax cos( w0t+
j) avec w0=[1/(LC)]½.
|
|
à t=0, x(0) = - Xm ;
d'où cos j=-1 et
j= p.
|
à t=0, q(0) = qmax ;
d'où cos j=0 et
j= 0.
|
|
w0=[2k/m]½
= 2 p/T0
doù T0 =2 p[m/(2k)]½
|
w0=[1/(LC)]½
= 2 p/T0
doù T0 =2 p[LC]½
|
Aspect
énergétique
:
|
t=0
|
ressort (r) compressé au maximum,
ressort (r') étiré au maximum ;
vitesse nulle. Les ressorts stockent
l'énergie sous forme potentielle
|
condensateur chargé au maximum,
intensité nulle. Le condensateur stocke
l'énergie ( électrostatique); la
bobine ne stocke pas d'énergie.
|
|
0,25
T0
|
Les ressorts ne sont pas
déformés ( position
d'équilibre ; la vitesse de m passe par un
maximum. La masse m stocke l'énergie sous
forme cinétique
|
condensateur déchargé ,
intensité maximale du courant. La bobine
stocke toute l'énergie (
électromagnétique)
|
|
0,5
T0
|
ressort (r') compressé au maximum,
ressort (r) étiré au maximum ;
vitesse nulle. Les ressorts stockent
l'énergie sous forme potentielle
|
condensateur chargé au maximum ( en
sens contraire de la charge
précédente) , intensité nulle.
Le condensateur stocke l'énergie (
électrostatique); la bobine ne stocke pas
d'énergie.
|
|
0,75
T0
|
Les ressorts ne sont pas
déformés ( position
d'équilibre ; la vitesse de m passe par un
maximum. La masse m stocke l'énergie sous
forme cinétique
|
condensateur déchargé ,
intensité maximale du courant. La bobine
stocke toute l'énergie (
électromagnétique)
|
|
T0
|
ressort (r) compressé au maximum,
ressort (r') étiré au maximum ;
vitesse nulle. Les ressorts stockent
l'énergie sous forme potentielle
|
condensateur chargé au maximum,
intensité nulle. Le condensateur stocke
l'énergie ( électrostatique); la
bobine ne stocke pas d'énergie.
|
|