Aurélie 03/04/07
 

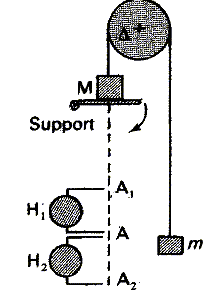
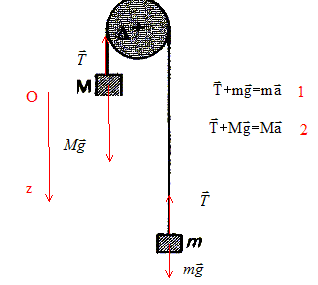
Concours Kiné : machine d'Atwood 2007 ( EFOM)

En poursuivant votre navigation sur ce site, vous acceptez l’utilisation de Cookies vous proposant des publicités adaptés à vos centres d’intérêts.

. .
.
.

 

Question 2 : 7 pts/20 sans calculatrice

Une machine d'Atwood se compose d'une poulie de masse négligeable, mobile sans frottement autour d'un axe horizontal D, et de deux solides de masse M et m( avec M>m), reliés par un fil inextensible, de masse négligeable, passant sur la poulie. On admet que la tension est la même de part et d'autre de la poulie.

  1. L'ensemble est immobilisé par un support placé sous le solide M. En faisant basculer ce support, on libère l'ensemble sans vitesse initiale. Etablir l'expression de l'accélération du mouvement en fonction de M, m et g.
    - Montrer que les mouvements de translation rectiligne verticaux de M et m sont uniformément accélérés. Justifier le sens du mouvement.
  2. On veut mesurer la valeur de cette accélération. Pour cela on utilise deux horloges H1 et H2 ; H1 mesure la durée q1 qui s'écoule entre les passages de M aux points A et A1 distants de d ; H2 mesure la durée q2 qui s'écoule entre les passages de M aux points A et A2 distants de d.
    - Etablir les équations qui régissent le mouvement de M.
    - En combinant ces équations, établir l'expression de l'accélération en fonction de d,     q1 et q2. 
En projection sur l'axe Oz :

1 s'écrit : T-mg=ma

2 s'écrit : Mg-T=Ma

éliminer T entre ces deux relations :(1) + (2)

(M-m) g=(M+m)a

a = g(M-m)/(M+m).

M>m donc a est positive : le mouvement s'effectue suivant Oz.

A est constante et positive : mouvement uniformément accéléré
Equations qui régissent le mouvement de M :

vitesse v = at ; distance z = ½at2 ; v2 = 2az

Au point A1 : z=½at2 (3)

Au point A : z+d = ½a(t+q1)2 (4)

Au point A2 : z+2d=½a(t+q1+q2)2 (5)

(4) -(3) donne : d=½a[(t+q1)2 -t2 ]=½aq1(2t+q1)

(5) -(4) donne : d=½a[(t+q1+q2)2-(t+q1)2 ]=½aq2(2t+2q1+q2)

q1(2t+q1) =q2(2t+2q1+q2)

2t(q1-q2) = q22-q12+2q1q2 ; 2t + q1 =( q22+q1q2) / (q1-q2)

or d= ½aq1(2t+q1) d'où d=½aq1q2( q2+q1) / (q1-q2)

a = 2d(q1-q2) / [q1q2( q2+q1)].
 

retour -menu