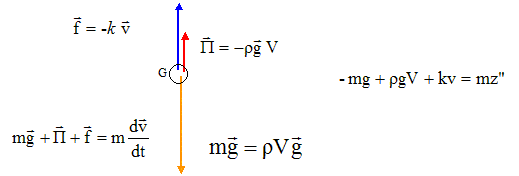Aurélie 21/05/07
 

Diplome d'accès aux études universitaires B vitesse limite de chute, carbone14, dipoles RLC. 2006

En poursuivant votre navigation sur ce site, vous acceptez l’utilisation de Cookies vous proposant des publicités adaptés à vos centres d’intérêts.

.
.

 

Exercice n°1 (6 points)

Une bille de volume V = 0,50 cm3 et de masse m = 1,5 g a un mouvement de chute verticale dans un liquide de masse volumique r = 0,80 g. cm-3.

Ce liquide exerce sur la bille une force de frottement de sens opposé à celui de la vitesse et de valeur f =k.v (k = 8.10-2 SI).

Donnée : g = 9,8 m.s-2.

  1. La poussée d'Archimède est-elle négligeable devant le poids ? Justifier.
  2. Etablir l'équation différentielle du mouvement.
  3. Déterminer la valeur de la vitesse limite.
Poids : mg = 1,5 10-3*9,8 =1,47 10-2 N.

poussée : poids du volume de liquide déplacé F= V r g avec V r 0,5*0,8 = 0,4 g = 4 10-4 kg.

F= 4 10-4 *9,8 = 3,92 10-3 N.

Le poids est voisin de 3,5 fois la poussée : la poussée n'est pas négligeable devant le poids.

La bille est soumise à son poids, à la poussée d'Archimède et à la force de frottements :

Ecrire la seconde loi de Newton sur un axe verticale orienté vers le haut.

L'équation différentielle relative à la vitesse s'écrit :

dv/dt -k/m v = g(rV/m-1).

Vitesse limite :

Lorsque la vitesse devient constante, dv/dt s'annule, d'où :

-k/m vl = g(rV/m-1).

vl =mg/ k (1- rV/m-).

vl = 1,5 10-3*9,8/0,08 ( 1-4 10-4 / 1,5 10-3) ; vl = 0,135 m/s.

Exercice n°2 (7 points)

DOCUMENT

La Terre est bombardée en permanence par des particules très énergétiques venant du cosmos. Ce rayonnement cosmique est composé notamment de protons très rapides. Les noyaux des atomes présents dans la haute atmosphère " explosent " littéralement sous le choc de ces protons très énergétiques et, parmi les fragments, on trouve des neutrons rapides. Ces neutrons rapides peuvent à leur tour réagir avec des noyaux d'azote de la haute atmosphère. Lors du choc, tout se passe comme si un neutron rapide éjectait un des protons d'un des noyaux d'azote et prenait sa place pour former un noyau Y1. Ce noyau Y1 est un isotope particulier du carbone, le carbone 14, qui est radioactif : en émettant un électron et une particule non observable, l'antineutrino, il se décompose en un noyau Y2. La période ou demi-vie du carbone 14 est 5 570 ans. Comme le rayonnement cosmique bombarde la Terre depuis longtemps, un équilibre s'établit entre la création et la décomposition du carbone 14 : il y a autant de production que de décomposition si bien que la teneur en carbone 14 de tous les organismes vivants reste identique au cours du temps. Ce carbone s'oxyde en dioxyde de carbone qui se mélange à celui de l'atmosphère, à celui dissous dans l'eau, etc. et sera métabolisé par les plantes et à travers elles par tous les organismes vivants. Dans chaque gramme de carbone de l'atmosphère ou des organismes vivants, les atomes de carbone sont en très grande majorité des atomes de carbone 12, mais il y a 6,8 . 1010 atomes de carbone 14.

D'après I. Berkès " La physique du quotidien ".

On donne, pour différents noyaux :

H : Z = 1 ; He : Z = 2 ; C : Z = 6 ; N : Z = 7 ; O : Z = 8.

1 an = 365 jours.

I - Réactions nucléaires dans la haute atmosphère

  1. Le proton est représenté par le symbole 11H. Justifier cette écriture.
  2. L'équation de la réaction qui a lieu lorsque le neutron rapide éjecte un des protons du noyau d'azote peut s'écrire :
    10n + 147N---> AZY1 + 11H
    - Énoncer les lois de conservation qui régissent une réaction nucléaire.
    - Vérifier que, comme l'indique le texte, on obtient bien du carbone 14 ; préciser la composition de ce noyau.
  3. Désintégration du carbone 14
    - Écrire l'équation de la réaction qui a lieu lorsque un noyau de carbone 14 se décompose à son tour, en précisant le type de radioactivité du carbone 14. On ne tiendra pas compte de l'antineutrino produit.
    - Identifier l'élément Y2 formé.
II- Phénomène de décroissance radioactive
  1. Donner la définition du temps de demi-vie t1/2.
  2. Constante radioactive
    - Donner la relation entre la constante radioactive l et le temps de demi-vie t1/2.
    - Par une analyse dimensionnelle, déterminer l'unité de l
    - À l'aide du texte, calculer sa valeur en unité SI, pour la désintégration du carbone 14.
  3. Soit N le nombre moyen de noyaux radioactifs restant dans un échantillon à la date t. Le nombre moyen de désintégrations pendant une durée Dt courte devant t1/2 est -DN (opposé de la variation de N). Ce nombre moyen de désintégrations est donné par la relation : -DN =l. N D t.
    - Déterminer le nombre de désintégrations par minute et par gramme de carbone d'un organisme vivant à partir du moment de sa mort.
  4. Même question pour un échantillon de 1 gramme et une durée de 1 seconde. Quelle unité peut-on attribuer à ce dernier résultat ?
III - Datation au carbone 14

 

  1. Comment expliquer que la quantité moyenne de carbone 14 par kilogramme de matière (ou teneur) reste constante pour tous organismes en vie ?
  2. Comment évolue la teneur en carbone 14 quand un organisme meurt ? Justifier la réponse.
  3. On date par la méthode du carbone 14 un morceau de sarcophage en bois trouvé dans une tombe de l'Égypte ancienne. Dans cet échantillon, on mesure en moyenne 10 désintégrations par minute et par gramme de carbone.
    - Déterminer le nombre de noyaux de carbone 14 subsistant dans cet échantillon.
    - Proposer un âge pour le bois de ce sarcophage.

     

I - Réactions nucléaires dans la haute atmosphère

Le proton est représenté par le symbole 11H.

Le proton est constitué d'une charge positive ( Z=1) et d'un seul nucléon (A=1).

L'équation de la réaction qui a lieu lorsque le neutron rapide éjecte un des protons du noyau d'azote peut s'écrire :
10n + 147N---> AZY1 + 11H
Conservation de la charge : 7 = Z+1 soit Z= 6 ( élément carbone).

Conservation du nombre de nucléons : 14+1=A+1 d'où A=14

Le noyau de carbone 14 compte 6 protons et 14-6 = 8 neutrons.


Equation de la réaction qui a lieu lorsque un noyau de carbone 14 se décompose à son tour :

146C = 147N + 0-1e radioactivité de type b-.

II- Phénomène de décroissance radioactive

Définition du temps de demi-vie t1/2.

Durée au bout de laquelle l'activité initiale est divisée par deux.

Relation entre la constante radioactive l et le temps de demi-vie t1/2.

lt1/2 = ln2.
ln 2 est sans dimension ; t1/2 est un temps en seconde ; l = ln2 / t1/2 donc l est l'inverse d'un temps, l est en s-1.

t1/2 =5570 *365*24*3600 = 1,75 1011 s.

l = ln2 /1,75 1011 = 3,96 10-12 s-1.

Nombre de désintégrations par minute et par gramme de carbone d'un organisme vivant à partir du moment de sa mort :

-DN =l. N D t = 3,96 10-12 *6,8 1010 *60 = 16,1.

Pour un échantillon de 1 gramme et une durée de 1 seconde, l'activité sera égale à : 16,1/60 = 0,27 Bq.

 

III - Datation au carbone 14

 

La quantité moyenne de carbone 14 par kilogramme de matière (ou teneur) reste constante pour tous organismes en vie du fait des échanges entre l'organisme et l'atmosphère

La teneur en carbone 14 diminue quand un organisme meurt : il n'y a plus d'échanges entre l'organisme et l'atmosphère.

On date par la méthode du carbone 14 un morceau de sarcophage en bois trouvé dans une tombe de l'Égypte ancienne. Dans cet échantillon, on mesure en moyenne 10 désintégrations par minute et par gramme de carbone.  

Nombre de noyaux de carbone 14 subsistant dans cet échantillon :

A= l N avec A= 10/60 = 0,167 Bq

N= A/l = 0,167 / 3,96 10-12 =4,2 1010 noyaux.
Age pour le bois de ce sarcophage.

N=N0 exp(-lt) ; ln(N0/N) =lt ;

t = ln(N0/N ) / l = ln (6,8/4,2) / 3,96 10-12 =1,22 1011 s = 3,86 103 ans.

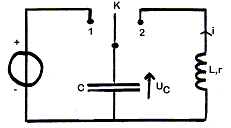
 On réalise le circuit correspondant au schéma :

Le condensateur de capacité C = 15 mF est préalablement chargé à l'aide d'un générateur idéal de tension continue (interrupteur en position 1). Il se décharge ensuite (interrupteur en position 2) à travers un circuit comportant une bobine d'inductance L = 1,0 H et de résistance r.

I - Étude du circuit

  1. Étude des oscillations :
    Un dispositif d'acquisition relié à un ordinateur permet de suivre pendant la décharge, d'une part l'évolution au cours du temps de la tension uC aux bornes du condensateur et d'autre part celle de l'intensité i du courant.

    - Déterminer à partir des courbes la valeur de la pseudo-période des oscillations.
    - Établir la relation entre l'intensité du courant i et la tension uC aux bornes du condensateur en respectant les conventions indiquées sur le schéma.
    - Entre les instants de dates tA et tB (voir figure 1), le condensateur se charge-t-il ou se décharge-t-il ? Justifier la réponse.

  2. Étude énergétique
    On souhaite étudier l'énergie totale E de l'oscillateur électrique. Cette énergie est la somme de l'énergie électrique E1 = ½ CuC2 emmagasinée dans le condensateur et de l'énergie magnétique E2 = ½ Li 2 emmagasinée dans la bobine. Le logiciel utilisé peut calculer, à partir des mesures, les valeurs de ces trois énergies et fournir les courbes donnant leur variation en fonction du temps.

    - L'origine des dates étant la même pour toutes les courbes des figures 1 et 2, identifier les trois courbes données figure 2 en ne justifiant que l'identification de la courbe donnant les variations de l'énergie magnétique.
    -Interpréter brièvement la décroissance de l'énergie totale de l'oscillateur électrique.

 

II Modélisation

On suppose maintenant que l'oscillateur ne comporte aucune résistance. Dans ces conditions, la tension uC aux bornes du condensateur est de la forme :

uC( t ) = Um sin (w0t + F) avec w0 = 2p/T0 = (LC)-½.

où T0 est la période propre de l'oscillateur.

  1. Calculer la valeur de T0.
  2. Établir les expressions :
    - de l'énergie électrique en fonction de C, Um, w0, F et t,
    - de l'énergie magnétique en fonction de C, Um, w0, F et t.
    - Montrer que, dans ce cas, l'énergie totale de I'oscillateur est conservée.
Étude du circuit

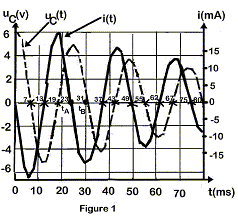
A partir des courbes la valeur de la pseudo-période des oscillations vaut : 2T = 49 ms ; T= 24,5 ms..
Relation entre l'intensité du courant i et la tension uC aux bornes du condensateur en respectant les conventions indiquées sur le schéma.

i = dq/dt avec q = CuC soit i = CduC/dt.
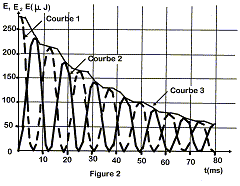
Entre les instants de dates tA et tB (voir figure ), la tension aux bornes du condensateur est décroissante : donc le condensateur se décharge à travers la bobine.

Étude énergétique
On souhaite étudier l'énergie totale E de l'oscillateur électrique. Cette énergie est la somme de l'énergie électrique E1 = ½ CuC2 emmagasinée dans le condensateur et de l'énergie magnétique E2 = ½ Li 2 emmagasinée dans la bobine. Le logiciel utilisé peut calculer, à partir des mesures, les valeurs de ces trois énergies et fournir les courbes donnant leur variation en fonction du temps.

Courbe 1 : E1 = ½ CuC2 à t=0, le condensateur stocke toute l'énergie du dipole LrC.

courbe 2 : E2 = ½ Li 2 à t =0,25 T, la bobine stocke toute l'énergie du dipole.

courbe 3 : E = E1+E2.

Lors des échanges d'énergie entre condensateur et bobine, une partie de l'énergie est perdue par effet joule dans les parties résistives : E décroît au cours du temps.

II Modélisation

On suppose maintenant que l'oscillateur ne comporte aucune résistance. Dans ces conditions, la tension uC aux bornes du condensateur est de la forme :

uC( t ) = Um sin (w0t + F) avec w0 = 2p/T0 = (LC)-½.

où T0 est la période propre de l'oscillateur.

T0 = 2p (LC)½ = 6,28(1*15 10-6)½ = 24,3 ms.

Expressions :
- de l'énergie électrique en fonction de C, Um, w0, F et t :

½CuC2 = ½C U2 m sin2 (w0t + F)
- de l'énergie magnétique en fonction de C, Um, w0, F et t :

½Li2 avec i = CduC/dt =C Um w0 cos(w0t + F)

½Li2 =½LC2 U2m w20 cos2(w0t + F)

Or LCw20 = 1 d'où ½Li2 =½C U2 m cos2 (w0t + F)
Energie totale de I'oscillateur :

½C U2 m cos2 (w0t + F) + ½C U2 m sin2 (w0t + F) = ½C U2 m = Constante.


retour -menu