Aurélie 04/06/07
 

concours électroradiologie médicale champ magnétique et forces électromagnétiques, ondes sur une corde. Caen 2007

En poursuivant votre navigation sur ce site, vous acceptez l’utilisation de Cookies vous proposant des publicités adaptés à vos centres d’intérêts.

. .
.
.

 

Cmposante horizontale du champ magnétique terrestre : Bh = 2 10-5 T ; perméabilité du vide m0 = 4p 10-7 u S.I.

N'ayant pas le document annexe, les schémas ont été imaginés à partir du texte.

A. étude de champs magnétiques.

  1. On a représenté le spectre magnétique d'un aimant droit :
    - Indiquer le pôole nord et le pôle sud de l'aimant. Justifier.
    - Représenter en O et en P le vecteur champ magnétique.
  2. A l'aide d'une boussole on a repéré la direction du champ magnétique terrestre en un lieu donné. Selon une direction perpendiculaire à celle du pôle nord magnétique, on approche de la boussole l'aimant droit. L'aiguille de la boussole tourne d'un angle q= 68 vers l'est.

    - Représenter le vecteur correspondant à la composante horizontale du champ magnétique terrestre, le vecteur champ magnétique de l'aimant et le vecteur champ magnétique résultant.
    - Exprimer puis calculer la valeur du champ magnétique crée par l'aimant.
    - Exprimer puis calculer la valeur du champ magnétique résultant.

  3. On veut reproduire au centre d'un solénoïde de longueur L = 50 cm, un champ magnétique Bsolénoide = 250 Bh, l'intensité du courant est I = 2,0 A.
    - Exprimer la valeur du champ magnétique au centre du solénoïde de longueur L comportant N spires et parcouru par le courant I.
    - Quelle est la valeur de N pour obtenir Bsolénoide = 250 Bh.
B. forces électromagnétiques :

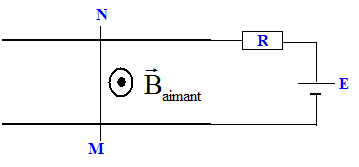
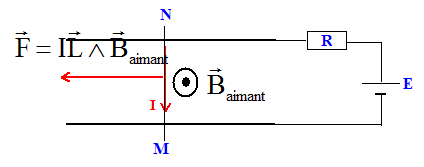
Le schéma représente en vue de dessus l'expérience des rails de Laplace. Le générateur a une fem E =6,0 V et une résistance interne R=0,30 ohm. La barre mobile MN, de résistance négligeable ferme le circuit entre le deux rails. Elle est placée dans l'entrefer d'un aimanr en U de largeur d= 40 mm, centré sur la barre, où règne un chmp magnétique uniforme de valeur B= 1,25 10-2 T.

  1. Indiquer le sens du courant dans la tige MN.
    - Déterminer l'intensité I.
  2. Représenter la force de laplace appliquée à la tige MN et calculer sa valeur.
    - Calculer le travail de cette force pour un déplacement L= 5,0 cm de la tige.
    - Que se passe t-il si on inverse les branchements aux bornes du générateur ?
C. Ondes sur une corde :

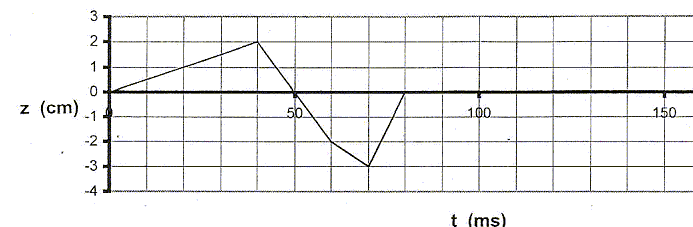
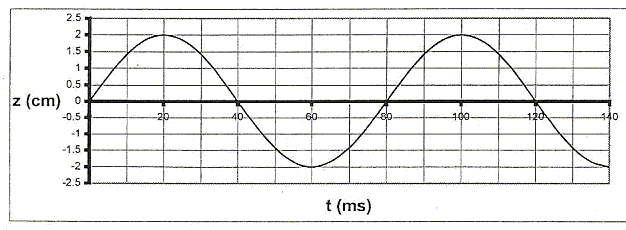
L'extrémité A d'une corde horizontale, initialement au repos, est perturbée verticalement. Cette extrémité A est choisie comme origine des abscisses. on donne sur la figure la représentation graphique de l'altitude z de A mesurée par rapport à la position de repos en fonction de la date t. Cette perturbation se propage le long de la corde à la célérité V= 2,0 m/s.

- Quel est le retard q, par rapport au point A, d'un point M d'abscisse x ? A quelle date le front d'onde arrive t-il au point B d'abscisse xB= 6,0 cm ?

La perturbation du point A est maintenant entretenue : c'est une fonction sinusoïdale du temps.

- Décrire l'aspect que prend la corde.

Déterminer la période du phénomène, sa fréquence, sa longueur d'onde.

A la date t1 = 0,8 s, quelle est l'altitude du point A ? Justifier.

Comparer l'état vibratoire d'un point D d'abscisse xD= 12 cm à celui du point C d'abscisse xC= 4 cm. Justifier.

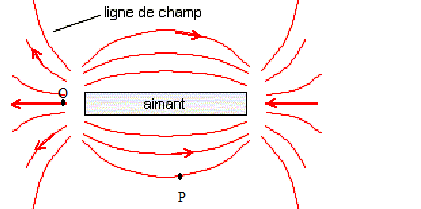
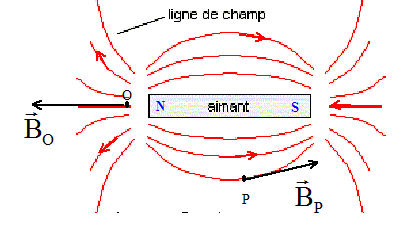
 A. Etude de champ magnétique :

A l'extérieur de l'aimant, les lignes de champ sont orientées du pôle nord vers le pôle sud ( elles rentrent au sud et sortent du nord).

Le vecteur champ magnétique est tangent à la ligne de champ, au point considéré ; ce vecteur a le sens de la ligne de champ.

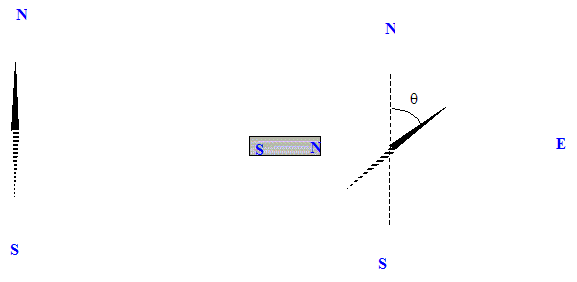
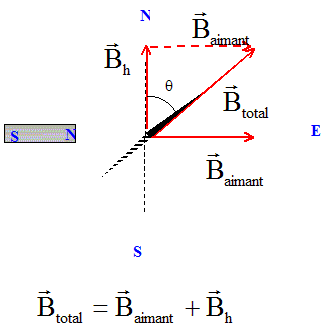
La boussole s'oriente suivant le champ magnétique total.

tan q = Baimant / Bh ; Baimant = Bh tan q = 2 10-5 * tan 68 = 5,0 10-5 T.

cos q = Bh / Btotal ; Btotal = Bh / cos q = 2 10-5 / cos 68 = 5,3 10-5 T.

Valeur du champ magnétique au centre du solénoïde de longueur L comportant N spires et parcouru par le courant I.

Bsolénoide = m0 N I / L.
Valeur de N pour obtenir Bsolénoide = 250 Bh.

N= 250 Bh L / (m0I) = 250*2 10-5 *0,5 /(4*3,14 10-7 *2) = 995 spires.

I = E/R = 6 / 0,3 = 20 A.

Le sens de la force de Laplace est donné par la règle des trois doigts de la main droite.

F= Baimant Id = 1,25 10-2 *20 * 0,04 = 0,010 N.

Travail de cette force pour un déplacement L= 5,0 cm de la tige.


W = F L = 0,01*005 = 5 10-4 J.

Si on inverse les branchements aux bornes du générateur, la tige MN se déplace dans l'autre sens.

 

Retard q, par rapport au point A, d'un point M d'abscisse x :

q = x/V = x/2 = 0,5 x.

A quelle date le front d'onde arrive t-il au point B d'abscisse xB= 6,0 cm ?

q= 0,5*0,06 = 0,03 s.

La perturbation du point A est maintenant entretenue : c'est une fonction sinusoïdale du temps.

La corde prend l'aspect d'une sinusoïde.

Période T = 80 ms = 0,08 s ; fréquence f= 1/T = 1/0,08 = 12,5 Hz ;

longueur d'onde l = VT = 2*0,08 = 0,16 m.

A la date t1 = 0,8 s, l'altitude du point A vaut :

zA(t) = 0,02 sin ( 2pt/T) = 0,02 sin (25 p t)

zA(0,8) =0,02 sin (25 p *0,8) =0,02 sin (20 p ) ; zA(0,8) = 0.

Comparer l'état vibratoire d'un point D d'abscisse xD= 12 cm à celui du point C d'abscisse xC= 4 cm.

C et D sont distants d'une demi longueur d'onde : C et D sont en opposition de phase.


retour -menu