Aurélie 05/04/07
 

Concours Kiné : rotation d'un cylindre, pendule 2007 ( Berck)

En poursuivant votre navigation sur ce site, vous acceptez l’utilisation de Cookies vous proposant des publicités adaptés à vos centres d’intérêts.

. .
.
.

 

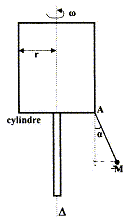
Question 2 : 5 pts/20

Le cylindre de rayon r est animé d'un mouvement de rotation uniforme autour de l'axe D. Un solide M de masse m considéré comme ponctuel est suspendu à un fil inextensible de longueur L en un point A de la circonférence du cylindre.

Le fil forme un angle a avec la verticale lorsque le cylindre tourne à la vitesse angulaire w constante. On néglige l'action de l'air.

r = 7,5 cm ; L= 10 cm ; m= 50 g ; a=20°.

  1. Représenter les forces qui s'exercent sur le solide M et le vacteur accélération a.
  2. Calculer la valeur de la tension F du fil.
  3. Etablir l'expression de l'accélération a du solide M en fonction de r, L, w et a.
  4. Calculer la valeur de w.
  5. Déterminer la période de rotation T( en s) du solide M autour de l'axe D.
 


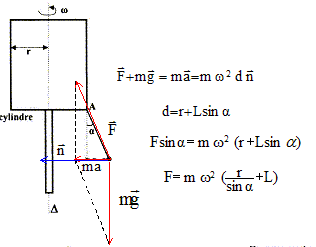
La tension F du fil vaut : F= mg/sina =0,05*9,8 / cos 20 = 0,52 N.

Expression de l'accélération a du solide M en fonction de r, L, w et a :

ma = F sin a = mw2(r+Lsin a).

a = w2(r+Lsin a).

valeur de w : tana = ma/(mg) = a/g ; a = g tan a ;

g tan a =w2(r+Lsin a) ; w = [g tan a / (r+Lsin a) ]½.

w = [9,81 tan 20 /(0,075 + 0,1 sin 20)]½ =5,7 rad/s.

période de rotation T( en s) du solide M autour de l'axe D :

T= 2p/w =6,28 / 5,7 =1,1 s.
 

retour -menu