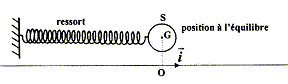Aurélie 05/04/07
 

Concours Kiné : QCM mécanique, électricité, optique, oscillateur, radioactivité 2007 ( Berck)

En poursuivant votre navigation sur ce site, vous acceptez l’utilisation de Cookies vous proposant des publicités adaptés à vos centres d’intérêts.

. .
.
.

 

Question 1 : 10 pts/20

On analyse tous les ans une source radioactive de césium 137. On détermine à l'instant t de l'analyse l'activité A(t) de la source.

On constate que A(t) / A(t+1) = 1,023 avec t en années.

Calculer le temps de demi-vie du césium 137. (10 ; 20 ; 30 ; 40 ; 50 ; aucune réponse exacte)

A(t) =A0 exp(-lt) ; A(t+1) =A0 exp(-l(t+1))

A(t) / A(t+1) = exp(-lt) exp(l(t+1)) = exp(l) ; l = ln(A(t) / A(t+1) = ln 1,023 = 2,27 10-2 an-1.

Or l t½=ln2 d'où t½=ln2 / l =ln2 / 2,27 10-2 = 30 ans.

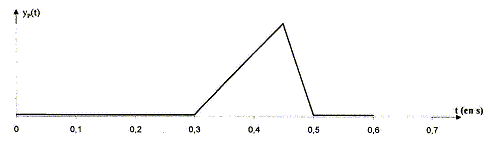
Une perturbation transversale se propage le long d'une corde tendue horizontalement. La déformation commence à l'instant t=0 en un point S. On considère un point P situé à la distance x=3,6 m du point S. Le mouvement de P est un mouvement rectiligne vertical suivant l'axe des y. On note yP(t) la représentation de la position de P en fonction du temps.

Calculer la célérité ( m/s) de la perturbation le long de la corde.(7,2 ; 12 ; 18 ; 24 ; 30 ; aucunne réponse exacte)

La perturbation atteint le point P, situé à une distance d= 3,6 m de la source avec un retard de 0,3 s ; d'où la célérité : 3,6 / 0,3 = 12 m/s.

Les niveaux d'énergie de l'atome d'hydrogène ont pour valeur En=-13,6 / n2 (eV).

h= 6,63 10-34 J s ; 1 eV= 1,6 10-19 J ; c= 3,00 108 m/s.

Parmi les affirmations suivantes combien il y en a-t-il d'exactes ?
- Le spectre d'émission de l'atome d'hydrogène est continu. faux.
- L'énergie minimale d'un électron capable de provoquer l'excitation d'un atome d'hydrogène à partir de son niveau fondamental vaut 10,2 eV.vrai.

La différence dénergie entre le premier niveau excité et le niveau fondamental vaut 13,6-13,6/4 = 10,2 eV. Le choc entre l'atome d'hydrogène et un électron d'énergie 10,2 eV conduit à l'excitation de l'atome.

- L'atome d'hydrogène peut émettre la radiation de longueur d'onde dans le vide l=122 nm en passant du niveau d'énergie n=2 au niveau n=1.vrai.

DE= 10,2 eV soit 10,2*1,6 10-19= 1,63 10-18 J

DE= hc/ l ; l=hc/DE= 6,63 10-34*3 108/1,63 10-18 =1,22 10-7 m = 122 nm.

- Le niveau d'énergie 0 eV correspond à l'atome d'hydrogène dans son niveau fondamental.faux.

niveau fondamental : n=1 et E=-13,6 eV ; atome ionisé E=0 eV.

- La valeur de l'énergie de l'atome d'hydrogène au niveau n=4 est de -1,36 10-19 J.vrai.

E4 = -13,6 / 16=-0,85 eV soit -0,85*1,6 10-19 = -1,36 10-19 J.

Une lentille convergente de distance focale f' = 25 cm donne d'un objet réel A, situé sur l'axe optique à 105 cm devant le foyer principal objet une image A'.

Calculer la distance (en cm) qui sépare A' du foyer principal image. (6,0 ; 8,0 ; 12 ; 16 ; 18 ; aucune réponse exacte)

Formule de conjugaison ( les distances algébriques sont écrites en bleu et en gras)

1/f' = 1/OA' - 1/OA avec OA = -(1,05+0,25 )=-1,3 m ; 1/f' = 1/0,25 = 4 d ;

1/OA' = 4+1/(-1,3) = 3,2 ; OA' = 0,31 m ; F'A' = 0,31-0,25 = 0,06 m = 6 cm.

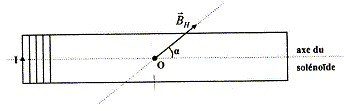
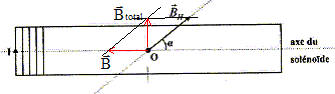
On place une aiguille aimantée en un point O à l'intérieur d'un solénoïde de longueur L=50 cm et comportant N=200 spires. En l'absence de courant, l'aiguille prend la direction de la composante horizontale BH du champ magnétique terrestre. Cette direction forme un angle de 45 ° avec l'axe du solénoïde. Lorsqu'on fait circuler un courant d'intensité I, on constate que l'aiguille tourne et forme un angle droit avec l'axe du solénoïde.

m 0=4p 10-7 S.I ; BH= 20 mT.

Calculer l'intensité du courant (mA) qui circule dans le solénoïde. (28 ; 56 ; 122 ; 188 ; 250 ; aucune réponse exacte)

B= Btotal = BH sin 45 = 2 10-5 cos45 = 1,41 10-5 T

de plus B= m 0N/L I soit I = BL/(m 0N)=1,41 10-5*0,5/(12,56 10-7*200)=2,81 10-2 A = 28 mA.
La planète Mars est assimilée à une sphère homogène de rayon R et à répartition de masse à symétrie sphérique. On a pu mesurer la force de gravitation exercée par mars sur une sonde spatiale de masse m à deux altitudes différentes : pour h1=4,82 104 km F1=40,2 N ; pour h2=7,76 104 km F2=16,3 N.

Calculer la valeur du rayon ( en km) de la planète Mars. (2,9 103 ; 3,1 103 ; 3,3 103 ; 3,52,9 103 ; 3,7 103 ; aucune réponse exacte)

F1= GMm/(R+h1)2 ; F2= GMm/(R+h2)2 ; F1/F2=[(R+h2) /(R+h1)]2

(R+h2) /(R+h1) =[F1/F2]½ ; [F1/F2]½ =[40,2/16,3 ]½ = 1,57 ;

1,57 (R+h1) =R+h2 ; R= (h2-1,57h1) /0,57 = (7,76 -1,57*4,82) 104/0,57 = 3,37 103 km.

Un oscillateur est constitué par un solide de masse m attaché à l'extrémité d'un ressort à spires non jointive, de masse négligeable et de constante de raideur k=8 N/m. Le solide S oscille sans frottement selon l'axe horizontale Ox. On repère la position, à l'instant t, du centre d'inertie G de S par l'abscisse x(t). L'origine O du repère correspond à la position du centre d'inertie G à l'équilibre.

L'équation horaire du mouvement s'écrit : x(t) = 8,00 10-2 cos(10,8 t + 0,723) avec les unités S.I.

Parmi les affirmations suivantes combien il y en a-t-il d'exactes ?

- A l'instant t=0, le solide est lâché sans vitesse initiale. faux.

x'(t) = -0,08*10,8 sin(10,8 t + 0,723) ; x'(0) = -0,08*10,8 sin(0,723)=-5,72 10-2 m/s.

- L'énergie mécanique de l'oscillateur est 7,2 mJ.faux.

Lorsque x=xm=0,08 m, l'énergie mécanique est sous forme potentielle élastique ½kxm2 =0,5*8*0,082 =2,56 10-2 J.

- La vitesse maximale du solide est 0,86 m/s.exact.

x'(t) = -0,08*10,8 sin(10,8 t + 0,723) ; x'm =0,08*10,8 =0,86 m/s.

- La masse du solide est 52 g. faux.

w0 = 10,8 rad/s ; w02=k/m ; m = k/w02=8/10,82 =6,86 10-2 kg = 68,6 g.

- L'accélération maximale du solide est 9,3 m/s². exact.

x"(t) = -0,08*10,82 cos(10,8 t + 0,723) ; x"m(t) = 0,08*10,82 = 9,3 m/s².

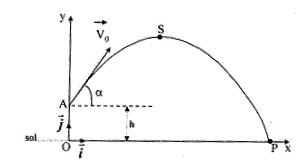
On lance un projectile considéré comme ponctuel, à partir d'un point A avec une vitesse initiale v0 faisant un angle a avec l'horizontale. On néglige l'action de l'air sur le projectile. h = 2,0 m ; yS=3,4 m ; xP=8,2 m.

Calculer a (°). 12 ; 27 ; 32 ; 41 ; 59 ; aucune réponse exacte.

équations horaires : x = v0cos a t ; y = -½gt2 +v0sin a t + h

vitesse : vx=v0cos a ; vy=-gt +v0sin a

en S : vy S=0 soit t = v0sin a / g ; repport dans y : yS =(v0sin a)2/ (2g) + h

3,4 = (v0sin a)2/ 19,62 +2 ; v0sin a = 5,24.

trajectoire : y = -½g x2 / (v0cos a)2 + x tan a + h

en P : 0 = -½*9,81* 8,22 / (v0cos a)2 + 8,2 tan a + 2

-329,8 / (v0cos a)2+ 8,2 tan a + 2 =0 ; remplacer v0 par 5,24 / sina d'où :

-12 tan2 a + 8,2 tan a + 2 =0 ; -12X2 +8,2X+2=0 avec X = tan a

la résolution donne : tan a =0,874 soit a = 41°.

En déduire la valeur de v0(m/s). 4,0 ; 8,0 ; 16 ; 24 ; 32 ; aucune réponse exacte)

v0 = 5,24 / sin a =5,24 / sin 41 = 8,0 m/s.

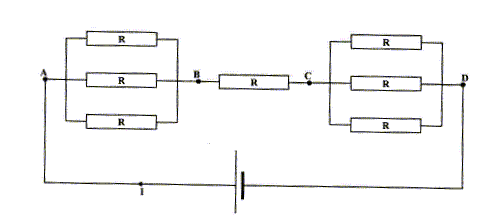
UAD=7,5 V

Calculer UBC (V). ( 1,0 ; 2,5 ; 3,5 ; 4,5 ; 7,5; aucune réponse exacte )

UBC =RI ; UAB=UCD=R/3 I=UBC /3.

additivité des tensions : UAD=UAB+UBC +UCD=UBC /3 + UBC + UBC /3 =5UBC /3

UBC =3UAD/5 =3*7,5/5 =4,5 V.
 

retour -menu