Aurélie 02/04/07
 

Concours Kiné : charge d'un condensateur 2007 ( Assas)

En poursuivant votre navigation sur ce site, vous acceptez l’utilisation de Cookies vous proposant des publicités adaptés à vos centres d’intérêts.

. .
.
.

 

Question 3 :

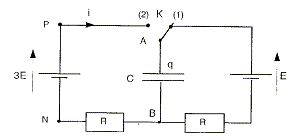
On étudie la chage q portée par l'armature A du condensateur.

Dans un premier temps, on charge le condensateur sous une tension E ( K en position 1 depuis très longtemps)

  1. Donner l'expression de la charge Q0 prise par l'armature A.
    A l'instant t=0 on bascule K en position 2.
  2. Quelle est la charge initiale q(0) de l'armature A ?
    - Quelle est l'expression de la charge finale q(oo) du condensateur ?
  3. Exprimer les intensité i(t) du courant et les tensions uAB(t) et uBN(t) en fonction de q(t) et de dq/dt.
    - En déduire l'équation différentielle à laquelle obéit q(t).
    - La solution de cette équation différentielle est de la forme q(t) = A+B exp(-t/    t) où A, B et t sont des constantes. Exprimer A et B en fonction des données. Comment se nomme t ? Donner son expression.
    - Représenter le graphe de q(t). Faire figurer la constante     t.
  4. Quelle est l'expression de l'intensité i(t) du courant ? Préciser sa valeur initiale.
    - Représenter le graphe de i(t). Faire figurer la constante     t.
 


Expression de la charge Q0 prise par l'armature A : Q0 =CE.

A l'instant t=0 on bascule K en position 2. La charge initiale q(0) de l'armature A est q(0) =Q0 =CE.
Expression de la charge finale q(oo) du condensateur : q(oo)= 3CE.

Expression de l'intensité i(t) du courant : i(t)=dq/dt = q'.

Expression de la tension uAB(t) : uAB(t) =q(t) / C.

Expression de la tension uBN(t) : uBN(t) =R i(t) ; uBN(t) = Rdq/dt.

Equation différentielle à laquelle obéit q(t) :

additivité des tensions : uAB(t) + uBN(t) = uAN(t) =3E

q/C+Rdq/dt =3E ; dq/dt + q/(RC) = 3E/R (1)
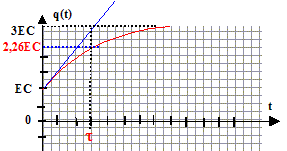
La solution de cette équation différentielle est de la forme q(t) = A+B exp(-t/t) où A, B et t sont des constantes.

t est la constante de temps et t =RC

Expressions de A et B en fonction des données :

dq/dt = -B/t exp(-t/t) ; repport dans (1) :

-B/t exp(-t/t) + A/t+B/t exp(-t/t) = 3E/R ; d'où A= 3E t /R ; A= 3EC.

Quant t 0, alors q(t) = EC et l'exponentielle vaut 1 d'où : EC=A+B ; EC= 3EC+B ; B= -2EC.

q(t) = EC[3-2exp(-t/t)].

A t= t la charge vaut : q(t) = EC(3-2 exp(-1)) =2,26 EC.

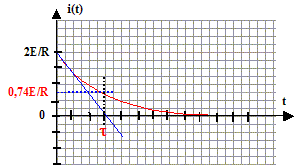
Expression de l'intensité i (t) du courant :

i = dq/dt = -B/t exp(-t/t) =2EC/(RC) exp(-t/t) ; i(t)= 2E/R exp(-t/t)

Valeur initiale : 2E/R.
 

retour -menu