Aurélie 08/06/07
 

concours assistant d'ingénieur téléobjectif, doublet de lentilles, lame à faces parallèles, miroir sphérique Cnrs 2006

En poursuivant votre navigation sur ce site, vous acceptez l’utilisation de Cookies vous proposant des publicités adaptés à vos centres d’intérêts.

. .
.
.

 

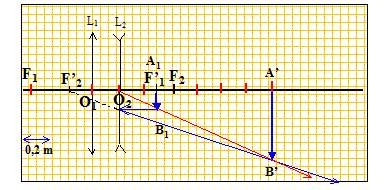
Un système optique est constitué de deux lentilles minces L1 et L2 séparée d'une distance e. La lentille L1 de centre O1 est convergente, de distance focale f'1.

La lentille L2 de centre O2 est divergente, de distance focale f'2.

  1. Le système est éclairé par une source à l'infini dans la direction de l'axe optique. A quelle condition un tel système forme t-il de ce point source une image réelle ?
  2. Cette condition étant satisfaite, on suppose que le système optique est éclairé par un objet plan situé à l'infini. Déterminer le sens de cette image par rapport à l'objet.
  3. Montrer que le système des deux lentilles est équivalent à une lentille mince convergente dont on calculera la distance focale.
    - Quel est l'intérêt d'un tel système ( téléobjectif) par rapport à une lentille convergente équivalente ?

- A. N : quelle est la distance focale image de la lentille convergente équivalente avec f'1 = 50 cm et f'2 = -40 cm et e = 20 cm ?

Si le système des deux lentilles est convergent, l'image d'un point source situé à l'infini est réelle.

L'image se forme au foyer principale image du système ; cette image est inversée par rapport à l'objet.

On notera AB l'objet, A1B1 l'image intermédiaire donnée par L1 de l'objet AB.

A1B1 joue le rôle d'objet pour la lentille L2 ; l'image définitive est notée A'B'.

L'objet étant à l'infini, l'image A'B' est situé au foyer image du système.

expression de la matrice de transfert :

matrice de réfraction sur le dioptre L2

V2 : vergence
matrice de translation O1O2 = e

milieu d'indice n =1
matrice de réfraction sur le dioptre L1

V1 : vergence
1 ;
0
-V2
1
1 ;
e /n
0
1
1 ;
0
-V1
1
matrice de transfert du doublet :

1 -eV1 ;............ e

-(V1+V2-eV1V2) ; 1-eV2.

Vergence du doublet : V= V1+V2-eV1V2.

avec V1 = 1/0,5 = 2 d ; V2 = 1/(-0,4) = -2,5 d ; e = 0,2 m

V = 2-2,5 + 0,2*2*2,5 = 0,5 d ; distance focale du doublet : f' = 1/0,5 = 2 m.

Intérêt d'un tel système ( téléobjectif) par rapport à une lentille convergente équivalente :

encombrement plus faible ( distance de la première lentille à l'image définitive) et l'image est plus grande.

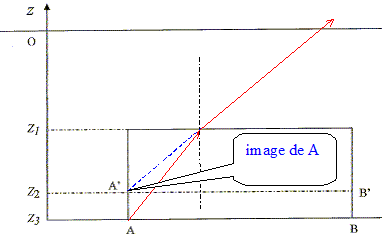
On pose une lame de verre à faes parallèles sur une surface plane. En utilisant un système optique adéquat, on vise la face supérieure et la face inférieure de la lame. Les positions successives du système optique sont lues sur un repère gradué, perpendiculaire au plan support, et l'on trouve : z1 = -11,9811 cm et z2 =-12,0012 cm.

Enfin on enlève la lame et l'on vise la surface du support. On trouve z3 = -12,0116 cm.

En déduire l'indice de réfraction de la lame.

Le déplacement de l'image A' par rapport à l'objet A a pour expression :

AA' = e( 1-1/n) avec e = z1-z3 et AA' = z2-z3.

AA'/e = 1-1/n ; 1/n = 1-AA'/e ; 1/n =( e-AA' )/ e

n = e/(e-AA') = (z1-z3) / (z1-z2).

n= (12,0116-11,9811) / ( 12,0012-11,9811) = 0,0305 / 0,0201 ; n = 1,5174.

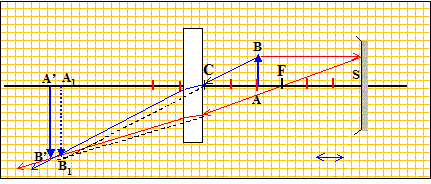
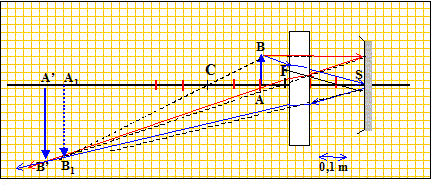
Les distances algégriques sont écrites en gras et en bleu.

Un point lumineux A est placé sur l'axe d'un miroir sphérique concave de sommet S et de centre C, avec SC= 60 cm. On a SA= 40 cm. Une lame à faces planes et parallèles de 9 cm d'épaisseur, et d'indice n= 1,5 est placée devant le miroir perpendiculairement à l'axe. Déterminer la position de l'image A' du point A :

- dans le cas où la lame est 60 cm devant le miroir.

- dans le cas où la lame est à 20 cm devant le miroir.

AB : objet ; A1B1: image intermédiaire donnée par le miroir sphérique ; A'B' : image définitive.

sens positif : celui de la lumière incidente ( le sens change après réflexion sur le miroir)

Relation de conjugaison pour le miroir avec origine au sommet :

1/ SA1 -1/ SA = -2/SC ; 1/ SA1 = -2/SC +1/ SA

avec SA = -0,4 m , SC = -0,6 m

1/ SA1 =2/0,6 + 1/(-0,4) =3,333-2,5 = 0,833.

SA1 =1,2 m.

A1B1 joue le rôle d'objet pour la lame à faces parallèles.

Le déplacement de l'image A' par rapport à l'objet A1 a pour expression :

AA1 = e( 1-1/n) = 0,09(1-1/1,5) =0,03 m

Il y a deux traversées de la lame ; le déplacement de l'image A' par rapport à l'objet A1 vaut 0,06 m.


retour -menu