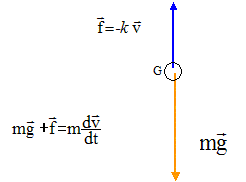|
concours kiné APHP
chute avec
frottements ; dipole RL; analogies
mécanique-électrique.
2007
|
|||||||||||||||||||||||||||||||||||||||||||||||||
| .
. |
|||||||||||||||||||||||||||||||||||||||||||||||||
|
|||||||||||||||||||||||||||||||||||||||||||||||||
|
Etude de la chute d'une balle soumise à des forces de frottements : On considère une balle de masse m ; cette balle est abandonnée dans l'air à l'instant t=0, sans vitesse initiale d'un point situé à une hauteur h au dessus du sol. On assimile les frottements à une seule force f = -kv. Bilan des forces subies par la balle en faisant un schéma. ( on négligera la poussée d'Archimède).
Equation différentielle vérifiée par la vitesse de la balle : Ecrire la deuxième loi de Newton sur un axe vertical orienté vers le bas : mg-kv=mdv/dt. dv/dt +k/m v = g. (1) de la forme dv/dt + a1 v = C avec a1 =k/m et C = g. Expression de t1et de vl : On admet que la solution peut s'écrire sous la forme v(t) = vl(1 - exp(-t/t1). dv/dt = vl /t1 exp(-t/t1) : repport dans (1) vl /t1 exp(-t/t1) +k/m vl(1 - exp(-t/t1) = g [vl /t1 -k/m vl ] exp(-t/t1) + k/m vl= g égalité vérifiée quelque soit le temps si : t1 = m/k et si vl= mg/k. t1 : constante de temps ( s) ; vl : vitesse limite de chute (m/s).
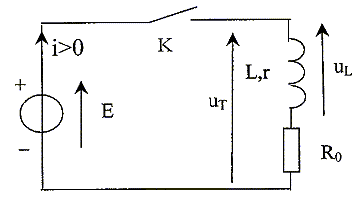
Etude du circuit électrique permettant la modélisation : On considère le circuit suivant, constitué d'une bobine d'inductance L et de résistance r en série avec une résistance réglable R0 et un interrupteur K, alimenté par un générateur idéal de fem E. A l'instant t=0 on ferme l'interrupteur K.
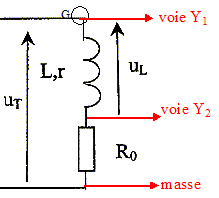
Branchements d'un oscilloscope permettant de visualiser la tension totale UT aux bornes du dipôle (L, r, R0) sur la voie Y1 et l'intensité i(t) du courant dans le circuit sur la voie Y2 :
La tension aux bornes d'un
résistor et l'intensité qui le traverse sont
proportionnelles : visualiser R0i c'est
visualiser l'intensité i(t) au facteur R0
près. Additivité des tensions : UT = E =UL + R0i avec UL = Ldi/dt + r i E= Ldi/dt + (R0+r) i = Ldi/dt + Ri di/dt + R/L i = E/L.
(2) En régime permanent l'intensité est constante et dI0/dt=0 d'où I0 = E/R. La solution de cette équation différentielle est du type i(t) = A+B exp(-a2t). Expressions de A, B, a2 en fonction de E, R et L : di/dt = -Ba2 exp(-a2t) ; repport dans (2) : -Ba2 exp(-a2t) +R/L(A+B exp(-a2t) = E/L B( -a2 +R/L) exp(-a2t)+AR/L= E/L. Egalité vérifiée quelque soit le temps si a2 =R/L et si A=E/R. De plus à l'instant t=0, l'intensité est nulle d'où B=-A. i(t) = E/R(1-exp(-R/Lt)). Dimension de a2 : énergie dégagée par effet Joule E=RI2t ; R= E/(I2t) : énergie /( intensité 2*temps) énergie stoickée par la bobine : E= ½LI2 ; L= 2E/I2 : énergie / intensité au carré. donc R/L a la dimension de l'inverse d'un temps.
UL = Ldi/dt + r i ; en régime permanent UL = rI0. Sur l'écran de l'oscilloscope, si le circuit avait été purement résistif on aurait observé une droite horizontale : U = RI0. La bobine s'oppose à
'établissement du courant.
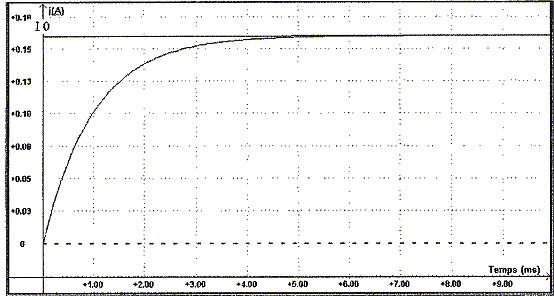
Les données de l'oscilloscope sont envoyées sur un logiciel de traitement des données. Après traitement on obtient à l'ordinateur la courbe suivante :
Tangente à l'origine de la courbe i(t) : Droite passant par l'origine, d'équation y = [di/dt]t=0 t. Or i(t) = E/R(1-exp(-R/Lt)) ; di/dt = E/Lexp(-R/Lt) ; [di/dt]t=0 = E/L y = Et/L ; si y =I0 alors t= t2 = LI0/E ; or I0 = E/R d'où t2 = L/R, constante de temps du circuit.
Principe de la simulation : On veut simuler la chute sans
vitesse d'une balle de masse m = 100 g dans le champ de
pesanteur g= 10 m/s2. Au bout d'une
durée
Dt la vitesse limite est
atteinte et prend la valeur 0,25 m/s. k = mg/0,25 = 0,1*10/0,25 =
4 kg
s-1. I0 = E/R Valeur qu'il faut donner à
la résistance R pour simuler le mouvement de la balle
étudiée : 4
W. E/L = 10 soit E = 10*0,1 =
1
V. On s'interesse à l'association des formes d'énergie électrique de la simulation et des formes d'énergie mécanique. On donnera les noms et les expressions mathématiques. vitesse limite vl intensité en régime permanent
I0 en régime transitoire, à la date t
: ½kv2 en régime transitoire, à la date t
½Ri2 Distance parcourue, notée d, par la balle au cours du régime transitoire : L'énergie stockée par la bobine correspond à 12,5 % de l'énergie consommée. Energie stockée par la bobine durant le régime transitoire : Pendant da durée dt : dW= Li di = L d(½i2) Intégrer entre 0 et I0 : W=½LI02 = 0,5 *0,1*0,252 =3,12 10-3 J Par suite, l'énergie consommée vaut : 3,12 10-3 / 0,125 = 0,025 J. Travail moteur du poids : mgd = 0,025 J d = 0,025/(0,1*10) = 0,025 m.
|
|||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||
|
|