Aurélie 18/06/07
 

Progression arithmétique, électricité, mécanique statique concours interne controleur des affaires maritimes 2004.

En poursuivant votre navigation sur ce site, vous acceptez l’utilisation de Cookies vous proposant des publicités adaptés à vos centres d’intérêts.

. .
.
.

On envisage la construction d'un ponton. Le coût du premier mètre est 250 euros hors TVA. Chaque mètre supplémentaire coûte 30 euros hors TVA, de plus que le mètre précédent. Le taux de TVA est 19,6 %. On dispose d'un budget de 18 420 euros toutes taxes comprises.

Déterminer la longueur du ponton qui peut être édifié.

Budget hors TVA : 18 420 /1,196 = 15401,33 euros.

Somme des termes d'une progression arithmétique : S= [2a + (n-1) r] ½n

a : premier terme, a = 250

r : raison, r = 30

n : nombre de terme

15 401,33 *2 = [500 +(n-1)*30] n

30 802,67  = 500 n + 30 n2 - 30 n

30 n2 +470 n- 30 802,67  =0

D = b2-4ac = 4702+4*30*30 802,67 = 3 917 220 ; D ½=1979,2

n = (-470 + 1979,2) / 60 = 25.
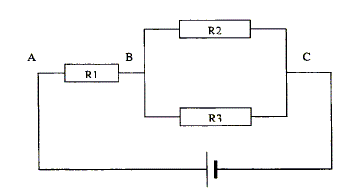
On considère l'association suivante dans laquelle R1=R2 = 20 W. R3 = 80 W. tension uAC= 18 V.

Déterminer la résistance équivalente au dipôle AC.

En déduire l'intensité du courant I1 dans R1.

Déterminer les tensions uAB et uBC.

Calculer les intensités des courants I2 et I3 traversant respectivement R2 et R3.

Vérifier les calculs précédents en utilisant la loi des noeuds.

R2 et R3 sont en dérivation : on peut les remplacer par une résistance unique de valeur R4 =R2R3/(R2+R3) = 20*80/100=16 W.

R1 et R4 en série sont équivalentes à : Réqui = R1 + R4 =20+16 = 36 W.

Intensité du courant I1 dans R1 :

I1 = uAC/ Réqui = 18 / 36 = 0,5 A.

Tensions uAB et uBC :

uAB = R1I1 = 20*0,5 = 10 V.

uBC = 18-10 = 8 V.

Intensités des courants I2 et I3 traversant respectivement R2 et R3 :

I2 = uBC/R2 = 8/20 = 0,4 A.

I3 = uBC/R3 = 8/80 = 0,1 A.

La loi des noeuds est bien vérifiée : I1 = I2+I3.

 

 

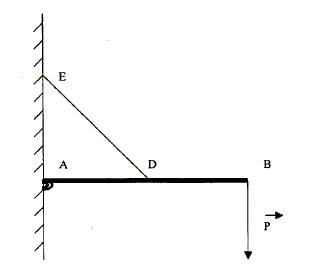
La barra AB rigide, de longueur AB= 4 m, est articulée en A. Elle est maintenue horizontale par un câble inextensible ED tel que ED=AD= 2 m.

Un poids de 1000 N est accroché en B. On néglige le poids de la barre et du câble.

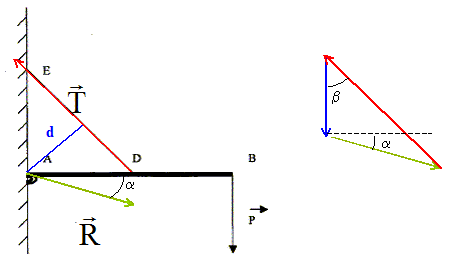
Déterminer la grandeur et la direction pat rapport à l'horizontale de la réaction du mur en A.

Ecrire que la somme des moments en A, des forces est nulle :

Le moment de R est nul, la force rencontre l'axe de rotation A.

Le moment de T vaut : -T*d avec d = ED/2 = AD/2½ = 1,414 m

Le moment de P vaut : +P*AB

d'où : P*AB - T d=0 ; T= P*AB/d = 1000*4 /1,414=2828 N.

b= 45 °

R2 = P2+T2-2PT cos b.

R2 = 106 + 28282-2*1000*2828*cos45 = 5 106 ; R = 2,24 103 N.

T2 = P2+R2-2PR cos (a+90).

28282 = 106 + 5 106 -2*1000*2240 cos (a+90)

cos (a+90) = -0,446 ; (a+90) 116,5 ° ; a = 26,5°.
 
retour -menu