Aurélie 6/05/07
 

Concours orthoptie Nantes 05 Circuit RL ; générateur de tension imparfait

En poursuivant votre navigation sur ce site, vous acceptez l’utilisation de Cookies vous proposant des publicités adaptés à vos centres d’intérêts.

..
.
.

 

On branche en série une pile de fem E, un interrupteur K, une bobine d'inductance L et de résistance R1 et un conducteur ohmique de résistance R2 = 50 W. Un ordinateur relié au montage permet d'enregistrer les tensions des voies A et B en fonction du temps.

  1. La pile a une résistance interne négligeable. A l'instant t=0 on ferme l'interupteur et on procède à lenregistrement.
    - Que visualise t-on sur la voie A ?
    - Etablir l'équation différentielle vérifiée par l'intensité i(t) du courant traversant le circuit.
    - La solution de l'équation différentielle est de la forme i(t) =a+b exp(-t/    t) où a, b et t sont des constantes. Déterminer a et t en fonction des paramètres du circuit. En déduire l'expression de i(t). Tracer la courbe obtenue lors de l'enregistrement sur la voie B.
  2. En réalité la pile possède une résistance interne r. Lors de l'enregistrement on obtient les courbes ci-dessous :

    - Identifier les deux courbes. Donner le fem de la pile.
    - Lorsque le régime est établi, l'intensité prend une valeur I0. Calculer I0, r et R1.
    - Le circuit est caractérisé par une constante de temps     t =L/R. Que représnte R ? Quelle est sa valeur ? Déterminer t à l'aide du graphe et en déduire L.
    - Calculer l'énergie emmagasinée par la bobine quand le régime permanent est établi.

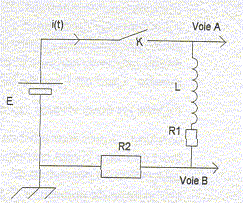
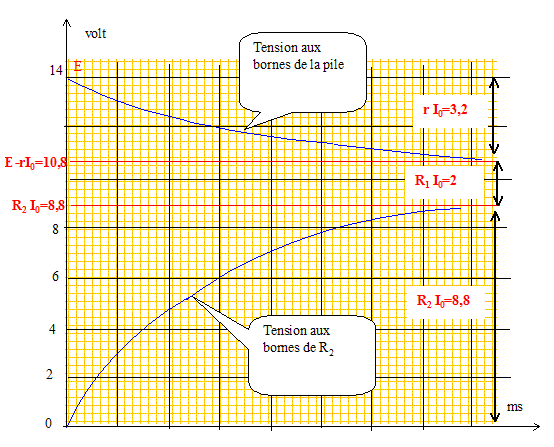
Sur la voie A on visualise la tension aux bornes de la pile.

Equation différentielle vérifiée par l'intensité i(t) :

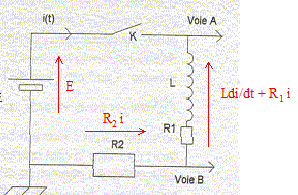
Additivité des tensions : E= Ldi/dt + R1i + R2i.

di/dt + (R1+R2)/L i = E/L (1)
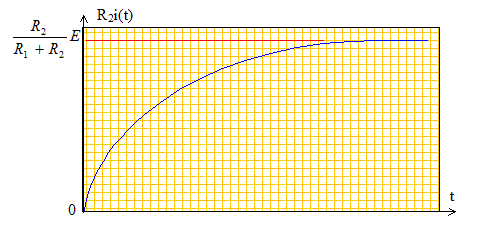
La solution de l'équation différentielle est de la forme i(t)= a+b exp(-t/t) où a, b et t sont des constantes.

di/dt = -b/t exp(-t/t) repport dans (1) :

-b/t exp(-t/t) +(R1+R2)/L(a+b exp(-t/t)) = E/L

[ -b/t+b(R1+R2)/L]exp(-t/t) +a(R1+R2)/L=E/L

égalité vérifiée quelque soit t si : a= E/(R1+R2) et si t = L/(R1+R2).

De plus à la date t=0 l'intensité est nulle d'où : 0 = a+b soit b=-a.

Expression de i(t) :

i(t) = E/(R1+R2)[1- exp(-t/t)].

Courbe obtenue lors de l'enregistrement sur la voie B :

On visualise la tension R2i(t) soit : u(t) =R2E/(R1+R2)[1- exp(-t/t)].

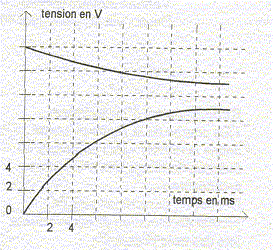
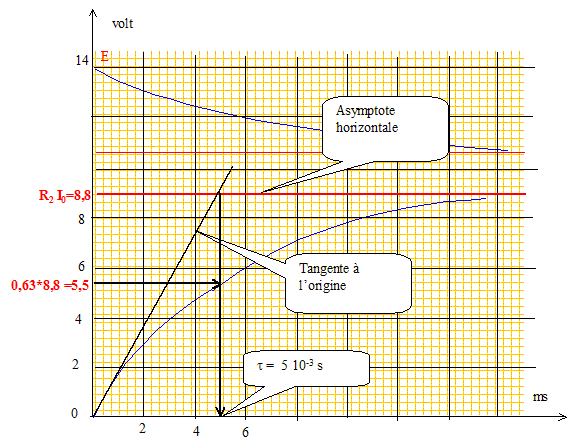
Lors de l'enregistrement on obtient les courbes ci-dessous :

Lorsque le régime est établi, l'intensité prend une valeur I0 telle que R2I0= 8,8 V.

 I0= 8,8/R2 =8,8 /50 ; I0= 0,176 A. ( I0=0,18 A)

r = 3,2/I0 =(3,2)/0,176 ; r = 18 W.

R1=2//I0 =2/0,176 ; R1= 11 W.

Le circuit est caractérisé par une constante de temps t =L/R.

R représente la somme des résistances R= r +R1+R2 =18+11+50 = 79 W.

 

Valeur de l'inductance L= t R = 5 10-3*79 =0,395; L= 0,40 H.


Energie emmagasinée par la bobine quand le régime permanent est établi :

W= ½LI02 ; W= 0,5*0,395*0,1762 =6,1 10-3 J.

 

retour -menu