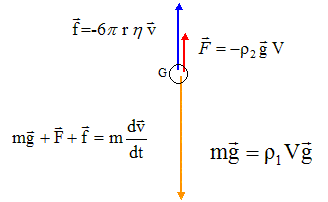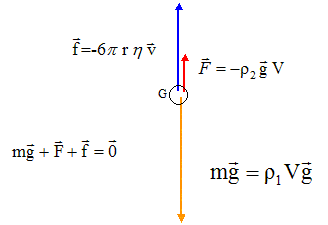Aurélie 27/04/07
 

Concours Capes interne : Viscosimètre à chute verticale 2007

En poursuivant votre navigation sur ce site, vous acceptez l’utilisation de Cookies vous proposant des publicités adaptés à vos centres d’intérêts.

. .
.
.

Les vecteurs sont écrits en gras et en bleu.  
Données (à pression atmosphérique et température normale)

masse volumique de l'acier r1=7,86 103 kg m-3, de la glycérine r2=1,26 103 kg m-3, ; g=9,81 m/s² ; rayon de la bille r= 5,0 mm.

Une bille en acier, sphérique, de rayon r, est maintenue immergée dans une solution de glycérine à l'aide d'un électroaimant. A l'instant t=0, on lâche la bille qui tombe verticalement. On étudie le mouvement dans le référentiel terrestre , supposé galiléen sur la durée de la chute.Les positions du centre d'inertie de la bille sont repérés sur un axe Ox, orienté vers le bas, muni d'un vecteur unitaire i et ayant pour origine O, position initiale du centre d'inertie de la bille.

Pour cette expérience, l'expression de la valeur de la force de frottement est donnée par la formule de stokes : f=6phrv.

r : rayon de la bille en mètre, v : vitesse de la bille (m/s, h : viscosité du fluide.

I. Bilan des forces :

  1. Qu'est-ce qu'un référentiel galiléen ?
  2. Retrouver par analyse dimensionnelle, l'unité S.I de la viscosité du fluide.
  3. Faire le bilan des trois forces qui s'appliquent à la bille.
  4. Donner l'expression vectorielle de chaque force en utilisant les notations de l'énoncé.
  5. Représenter ces forces sur un schéma ( sans échelle mais en respectant la direction et le sens de leur somme vectorielle)

II. Equation différentielle du mouvement :

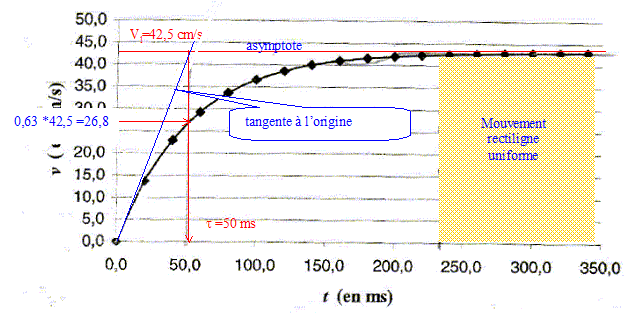
  1. Montrer que l'équation différentielle régissant le mouvement est du type dv/dt = A+Bv où A et B sont des constantes. Donner l'expression littérales de ces constantes en fonction des données.
  2. Vérifier que A = 8,24 m s-2.

III. Exploitation d'une chronophotographie :

Une chronophotographie a permis de tracer l'évolution de la vitesse en fonction du temps.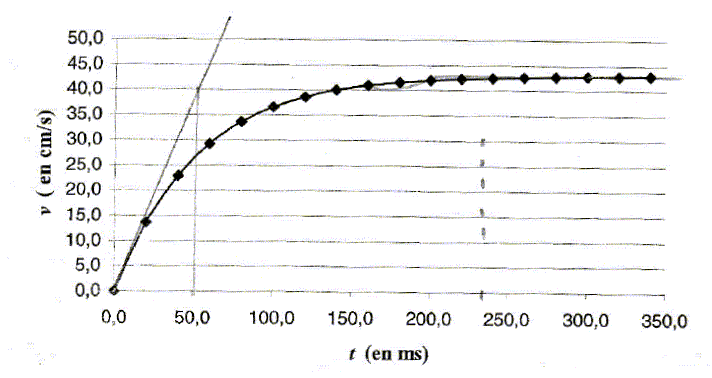

 Une modélisation ultérieure donne l'évolution de la vitesse de la forme : v(t) = vl(1-exp(-t/t)).

  1. Décrire la méthode qui permet, à partir d'une chronophotographie, de mesurer la vitesse instantanée d'n mobile.
  2. Définir vl et t. Donner leur unités. Déterminer graphiquement les valeurs de ces deux grandeurs.
  3. Exprimer vl et t en fonction de A et B.
  4. A partir de la mesure de vl et des données, calculer la viscosité h de la glycérine. Les tables donnent h théorique = 0,83 Pa s. Comparer la valeur expérimentale et la valeur théorique ( on calculera l'écart relatif). L'unité proposée correspond-elle à l'unité S.I déterminée précédemment ?
  5. Déterminer graphiquement la date t1 à partir de laquelle la vitesse devient constante. Quelle est la position x(t1) de la bille ? le régime transitoire est-il facilement observable à l'oeil nu ?
  6. Proposer un protocole pour mesurer la viscosité d'un liquide à partir d'une seule mesure de vitesse.

IV. Etude énergétique :

Soit un point C tel que xC= 15 cm.

  1. Déterminer l'expression puis la valeur du travail de chaque force appliquée à la bille, autre que la force de frottement, lors du déplacement OC.
  2. En supposant que la vitesse de la bille en C est vC=0,43 m/s, calculer le travail de la force de frottement.
I. Bilan des forces :

référentiel : objet par rapport auquel on se repère pour l'étude du mouvement d'un système ; on lui associe un repère et une origine des temps.

référentiel galiléen : dans ce référentiel le principe d'inertie ou 1ère loi de Newton s'applique " un point matériel pseudo-isolé demeure dans son état de repos ou de mouvement rectiligne uniforme".

 Retrouvons par analyse dimensionnelle, l'unité S.I de la viscosité du fluide :

f : force ou masse * accélération ou masse * longueur / temps2 ; [f]= M L T-2.

6p : sans dimension ; r : longueur ; [r]= L. ; v : vitesse ou longueur / temps ; [v]= L T-1.

h= f/(6p rv) ; [h]= M L T-2L -1 T L-1 ; [h]= ML -1T-1

Bilan des trois forces qui s'appliquent à la bille :

poids : vertical, vers le bas, valeur mg avec m = 4/3pr3r1 ; P= 4/3pr3r1 gi.

Poussée d'archimède : verticale, vers le haut, valeur 4/3pr3r2g ; F= 4/3pr3r2 g(-i).

frottement : vertical, vers le haut ; f=6phrv(-i).
t <0,25 s
t >0,25 s
II. Equation différentielle du mouvement :

La seconde loi de Newton ( écrite ci-dessus) s'écrit, suivant l'axe Ox : mg-F-f=mdv/dt

4/3pr3r1 g-4/3pr3r2 g -6phrv = 4/3pr3r1 dv/dt

g(1-r2 /r1)-4,5h/(r2r1) v = dv/dt

A=g(1-r2 /r1) ; B= -4,5h/(r2r1).

A = 9,81(1-1,26/7,86)=8,24 m s-2.

III. Exploitation d'une chronophotographie :

Apartir d'une chronophotographie, la vitesse instantanée d'un mobile se calcule à partir de :

v(ti) = [OMi+1-OMi-1] / (2Dt).

Dt durée petite, intervalle de temps séparant deux chronophotographies successives.

vl : vitesse limite de chute ( m/s) ; t : constante de temps (s).

Expression de vl et t en fonction de A et B :

v(t) = vl(1-exp(-t/t)) ; dv/dt = vl/t exp(-t/t) ;

repport dans l'équation différentielle : dv/dt = A+Bv

vl/t exp(-t/t) =A+Bvl(1-exp(-t/t))

Expression vérifiée quel que soit t si : A+Bvl = 0 soit vl = -A/B et si t = -1/B.

Calculer la viscosité h de la glycérine :

B = -A/vl = -8,24 / 0,425 =-19,4 s-1 ; or B= -4,5h/(r2r1)

d'où h=-Br2r1/4,5 = 19,4*(5 10-3)2 *7,86 103/4,5 ; h= 0,847 kg m-1 s-1.

Les tables donnent h théorique = 0,83 Pa s.

Ecart relatif : (0,847-0,83)/0,83 *100 = 2 % ( donc accord entre valeurs expérimentale et théorique)

L'unité proposée correspond à l'unité S.I déterminée précédemment :

pression (Pa) = force (N) / surface (m2) = masse *accélération / surface ;

[pression * temps]=M L T-2 L-2 T = ML -1T-1

A partir de la date t1 =250 ms la vitesse devient constante. La position x(t1) de la bille est :

v(t) = vl(1-exp(-t/t)) ; par intégration x(t) = vlt + vltexp(-t/t) + Cte

Calcul de la constante : x(0) = vlt + Cte ; Cte = -vlt

à t = 250 ms le terme vltexp(-t/t) s'annule d'où x(t1) =0,425*0,25 - 0,425 *0,050 = 0,085 m = 8,5 cm.

Le régime transitoire est facilement observable à l'oeil nu.

Protocole pour mesurer la viscosité d'un liquide à partir d'une seule mesure de vitesse :

Lorsque la vitesse limite est atteinte, mesurer la durée Dt correspondant au passage de la bille devant deux repères distants de d= 40 cm par exemple.

d'où vl = d/Dt puis procéder comme ci-dessus.

IV. Etude énergétique :

Soit un point C tel que xC= 15 cm.

Expression puis valeur du travail moteur ( descente) du poids, force constante, lors du déplacement OC :

W1= P*OC= 4/3pr3r1 g xC ; W1=4/3*3,14*(5 10-3)3*7,86 103 *9,81*0,15=6,1 10-3 J.

Expression puis valeur du travail résistant de la poussée d'Archimède, force constante, lors du déplacement OC :

W2= -F*OC= - 4/3pr3r2 gxC ; W2=-9,7 10-4 J.

En supposant que la vitesse de la bille en C est vC=0,43 m/s, calcul du travail de la force de frottement :

théorème de l'énergie cinétique : ½mv2C-0 = W1+W2+Wf.

Wf =½mv2C- W1-W2 ; avec m = 4/3pr3r1 = 4,11 10-3 kg.

Wf = 0,5*4,11 10-3 *0,432 -6,1 10-3 + 9,7 10-4 = -4,7 10-3 J.
 

retour -menu