|
Oscillations électriques libres Capes 2000 En poursuivant votre navigation sur ce site, vous acceptez l’utilisation de Cookies vous proposant des publicités adaptés à vos centres d’intérêts.
|
|
| .
. |
|
|
|
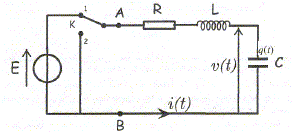
Lorsque le commutateur K est en position 1, le condensateur se charge sous la tension E délivrée par un générateur de tension constante. Le condensateur une fois chargé, on bascule à l'instant t=0 le commutateur en position 2. Equation différentielle vérifiée par la tension v(t) aux bornes du condensateur : additivité des tensions : v(t) = R i(t) + Ldi(t) /dt De plus i(t) = - dq(t) / dt avec q(t) = C v(t) d'où i(t) = -C dv(t)/dt ; di(t)/dt = -C d2v(t)/dt2. Par suite v(t) = -R C dv(t)/dt - LC d2v(t)/dt2. d2v(t)/dt2+ R/Ldv(t)/dt +1/(LC) v(t) = 0. En posant or w0 = (LC)-½ et Q0 = 1/R [L/C]½ soit w0 /Q0 =R/L. v"(t) +w0 /Q0 v'(t) +w02 v(t) =0. (1) Conditions initiales de décharge du condensateur : L'énergie stockée par le condensateur et en conséquence la tension aux bornes du condensateur sont continues. v(0-) = v(0+) = E. L'énergie stockée par la bobine et en conséquence l'intensité du courant sont continues. i(0-) = i(0+) = 0. Afin d'avoir une forme réduite de l'équation différentielle, on introduit la grandeur t = t/(LC)½ et le degré d'amortissement a = ½R (C/L)½. dt/dt = 1/(LC)½ = w0 ; dv(t) / dt = dv(t)/dt * dt/dt = w0 dv(t)/dt ; d2v(t)/dt2 = w02 d2v(t)/dt2 a = ½R (C/L)½ = 1/(2Q0 ) ; 1/Q0 =2 a. L'équation différentielle (1) s'écrit alors : w02 d2v(t)/dt2 + 2a w02 dv(t)/dt + w02 v(t) =0 Diviser chaque termes par w02 , grandeur non nulle : d2v(t)/dt2 + 2a dv(t)/dt + v(t) =0 (2)
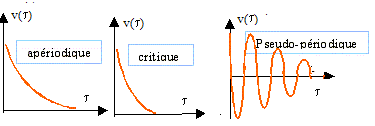
Suivant les valeurs du degré d'amortissement a il existe deux régimes principaux d'évolution de la tension v(t) : L'équation caractéristique associée à (2) s'écrit : r2 + 2a r = 1 =0 ; discriminant réduit D' =a2-1 Si a>1 , régime apériodique Si a<1 , régime pseudopériodique.
Pour L= 0,04 H et C= 22 nF calculons cette valeur Rcritique. Or a = ½R (C/L)½ d'où 1 =½Rcritique (C/L)½ ; Rcritique = 2(LC)½ ; Rcritique = 2 (0,04 / 22 10-9)½ =2,7 103 W. |
|
|
|
|
|
|