|
Concours ca/plp externe : repérage de température ; sonde de platine Pt100 2007 En poursuivant votre navigation sur ce site, vous acceptez l’utilisation de Cookies vous proposant des publicités adaptés à vos centres d’intérêts. |
|||||||||||||||||||||||||
| .
. |
|||||||||||||||||||||||||
|
|||||||||||||||||||||||||
|
I. Le thermomètre à liquide : Il est constitué d'un réserve de liquide surmonté d'un long tube fin. Historiquement le liquide était de l'alcool pais on peut aussi utiliser du mercure. La construction de ce genre de tube a été réalisée au début du XVIIIè siècle, mais encore fallait-il graduer le tube.
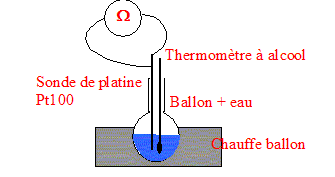
La résistance électrique d'un conducteur métallique croît avec la température. Cette variation de résistance est réversible. Comme métal, on peut utiliser l'or, le cuivre, le nickel ou le platine. Un protocol expérimental
propose de plonger une sonde de platine et un
thermomètre à alcool ( supposé
correctement étalonné ) dans un ballon
contenant de l'eau. Un chauffe ballon permet d'élever
progressivement la température de l'eau et un
omhmètre est utilisé pour mesurer la
résistance de la sonde de platine. On obtient le
tableau de mesures ci-dessous : R(q) = R0[1+Aq + Bq2 +Cq3(q-100)], où q est la rempérature en °C. R0 = 100 W ; A= 3,9083 10-3 S.I ; B=-5,775 10-7 S.I ; C= -4,183 10-12 S.I Les sondes de platine Pt100 présentent l'avantage de posséder une bonne linéarité, c'est à dire que le modèle linéaire R(q) = R0[1+Aq] est une bonne approximation de la relation complète.
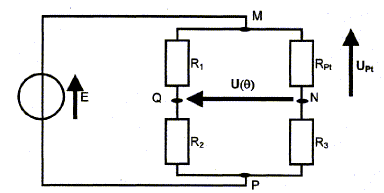
La sonde Pt100 ( symbolysée par le conducteur ohmique de résistance RPt) est insérée dans le montage suivant :
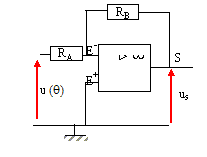
L'intérêt de ce circuit est de convertir une information " résistance" en information "tension". La notice précise qu'il faut éviter les intensités supérieures à 3 mA, car un risque d'auto-échauffement excessif de la sonde préjudiciable à la mesure existe alors ( élévation de température de 0,5 K quand l'intensité traversant la sonde est de 3 mA).
I. Le thermomètre à liquide : L'échelle Celsius utilise pour sa définition deux phénomènes physiques auquels on attribue les températures 0°C et 100°C : fusion de la glace et ébullition de l'eau sous une pression de 1 bar. L'échelle Celsius est qualifiée de "centésimale". L'intervalle de température repéré par les deux phénomènes physiques est divisé en 100 graduations. Une des propriétés physiques remarquable du mercure : liquide à température ambiante sous une pression de 1 bar. Les thermomètres médicaux à mercure sont interdits à la vente depuis 1998. En cas de casse, le mercure se répand sur le sol ; il est difficile à récupérer ; il s'évapore lentement, les vapeurs étant nocives. II. Etalonnage d'une sonde de platine ( Pt100) : La résistance de la sonde de platine est donnée par la relation : R(q) = R0[1+Aq + Bq2 +Cq3(q-100)], où q est la rempérature en °C. unité de A : Aq est sans dimension, q est en °C donc A est en °C-1. unité de B : Bq2 est sans dimension, q est en °C donc B est en °C-2. Schéma annoté du dispositif expérimental qui a permis de dresser le tableau :
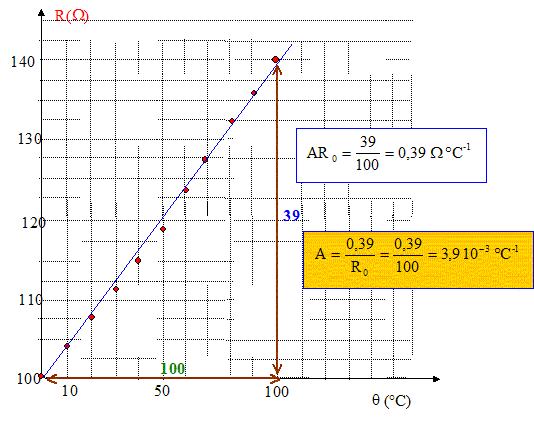
On sélectionne le bon calibre d'un ohmètre en commençant par le plus grand, puis en diminuant ; on s'arrête au calibre précédent celui qui indique 1. Valeur expérimentale Aexp de A :
A (théorique) et
Aexp sont identiques. Ce résultat confirme
que le modèle linéaire constitue une
très bonne approximation de la relation
complète.
III. Mesure de température à l'aide d'une sonde de platine ( Pt100) : " K" dans "0,5 K" signifie Kelvin. Relation reliant une température exprimée en K et la même exprimée en °C : température en Kelvin = 273 + température en Celsius. La partie du circuit, située entre M et P et constituée de conducteurs ohmiques est un "pont de conducteurs ohmiques ". Expression de UPt en fonction de E et de certaines résistances constituant le circuit : UPt=UMN=UMP+UPN =UMP-UNP = E-R3IPt. de plus E= (RPt+R3)IPt soit IPt =E/(RPt+R3) d'où UPt= E-R3=E/(RPt+R3) ; UPt= ERPt/(RPt+R3) Expression de l'intensité IPt circulant dans la sonde de platine : IPt =E/(RPt+R3) Expression de U1 =UMQ en fonction de E et de certaines résistances constituant le circuit : U1=UMQ=UMP+UPQ =UMP-UQP = E-R2I1. Or E= (R1+R2)I1 soit I1 =E/ (R1+R2) U1= E-R2E/ (R1+R2) ; U1=R1E/ (R1+R2) Expression U(q) en fonction de E, R0, R1, R2, R3, A et q : U(q) =UQN= UQM+UMN= -UMQ+UMN= UPt-U1=ERPt/(RPt+R3) -R1E/ (R1+R2) avec RPt =R(q) = R0(1+Aq) U(q)
=
E[R0(1+Aq)/(R0(1+Aq)+R3)
-R1/
(R1+R2)]. U(0)=10[100/200-100/200) ; U(0)= 0 V. IPt
=E/(R0(1+Aq)+R3)
; IPt
=10/200 ;
IPt =0,05
A. U(100)=10[140/240-100/200) ; U(100)= 0,83 V. IPt
=E/(R0(1+Aq)+R3)
; IPt
=10/240 ;
IPt =0,042
A. L'effet Joule permet d'expliquer l'auto-échauffement. Pour diminuer le phénomène
d'auto-échauffement, un professeur conseille de
diminuer E et d'augmenter R1 et R2.
Ces choix ne sont pas sans conséquences sur
U(q) : pour certaines valeurs de
E, R2 et R3 ( différentes de
celles utilisées dans l'énoncé), cette
tension varie alors seulement de 0 mV à 32 mV.
|
|||||||||||||||||||||||||
|
|
|||||||||||||||||||||||||
|
|