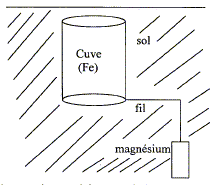
Protection électrochimique d'une cuve enfouie dans le sol BTS travaux publics 2007

En poursuivant votre navigation sur ce site, vous acceptez l’utilisation de Cookies vous proposant des publicités adaptés à vos centres d’intérêts.

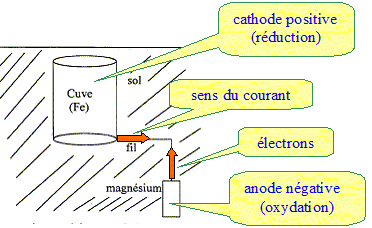
Données : potentiel standard des couples redox E°(Fe²⁺ / Fe) = -0,44 V ; E°(Mg²⁺ / Mg) = -2,37 V

Masse molaire ( g/mol) Fe : 55,8 ; Mg : 24,3 ; 1 F = 9,65 10⁴ C

Ecrire et équilibrer les demi-équations électroniques qui se produisent sur l'électrode de magnésium et sur la cuve.

Indiquer l'oxydation et la réduction.

Oxydation du magnésium : Mg = Mg²⁺ + 2e^-.

Réduction des ions Fe²⁺ ( au niveau de la cuve) : Fe²⁺+ 2e^- = Fe.

Compléter le schéma en indiquant le sens de circulation des électrons, le sens de l'intensité du courant, le pôle +, le pôle-, l'anode, la cathode.

Explique pourquoi le magnésium est capable de protéger le fer.

Le magnésium est un métal plus réducteur que le fer : E°(Mg²⁺ / Mg) <E°(Fe²⁺ / Fe)

Le magnésium s'oxyde à la place du fer ; ce dernier est donc protégé tant qu'il y a du magnésium.

Calculer la durée Dt de cette protection, exprimée en secondes puis en années.

Quantité de matière (mol) de magnésium = masse (g) / masse molaire (g/mol)

n(Mg) = m/M= 200 / 24,3 = 8,23 mol

Or Mg = Mg²⁺ + 2e^-.

donc la quantité de matière d'électrons est égale à : n(e^-) = 2 n(Mg) = 16,5 mol ( 16,460)

La quantité d'électricité traznsportée par une mole d'électrons est : 96500 C

Quantité d'électricité Q = 96500 * n(e^-) = 96500*16,46 = 1,59 10⁶ C ( 1,5885 10⁶)

Quantité d'électricité Q = IDt  avec I= 0,015 A

Dt = 1,5885 10⁶ / 15 = 1,06 10⁸ s soit 3,36 ans.

Quelle serait la masse de fer qui disparaîtrait pendant la même durée, dans les mêmes conditions si la cuve n'était pas protégée ?

n(Fe) = n(Mg) = 8,23 mol

masse (g) = masse molaire du fer (g/mol) * quantité de matière (mol)

m(fer) = 55,8*8,23 = 459 g.