Aurélie 13/10/07
 

élément titane : structure, métallurgie, diagramme Ellingham, diagramme potentiel-pH BTS chimiste 2007

En poursuivant votre navigation sur ce site, vous acceptez l’utilisation de Cookies vous proposant des publicités adaptés à vos centres d’intérêts.

. .
.
.

 

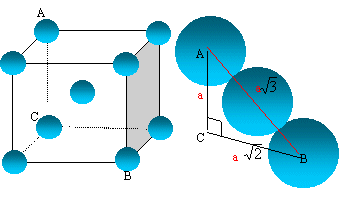
L'atome de titane :

Donner la structure électronique d'un atome de titane dans son état fondamental et justifier la position de l'élément titane dans la classification électonique.

Le n° atomique Z vaut Z= 22, donc 22 électrons

1s2 2s2 2p6 3s2 3p6 4s2 3d2.

Le niveau n= 4 est partiellement occupé, l'élément titane appartient à la 4ème ligne ( période) de la classification périodique.

4s2 3d2 : 4 électrons externes, le titane appartient à la 4ème colonne.

A quelle catégorie cet élément appartient-il ?

1ère série des métaux dits de "transition".

Indiquer la structure électronique de l'ion Ti2+. Préciser le nombre d'électrons célibataires pour cet ion.

1s2 2s2 2p6 3s2 3p6 3d2.

3d2 : deux électrons célibataires.

Le métal titane :

La variété de titane solide stable au dessus de 882° C est le titane b qui cristallise dans le réseau cubique centré.

Représenter le schéma de la maille.

Exprimer puis calculer le rayon métallique R de l'atome de titane ( masse volumique du titane r = 4327 kg m-3 )

 

Les 8 atomes situés aux sommets du cube sont communs à 8 mailles et comptent pour 1/8=0,125 chacun

celui du centre, commun à une seule maille, compte pour une unité.

nombre d'atomes de titane appartenant à la maille : 8* 0,125 +1 = 2.

Masse d'une maille : masse de deux atomes de titane = 2*masse molaire (kg) /nombre d'avogadro

m = 2MTi / NA.

volume d'une maille : V= a3

La tangence s'effectue suivant la grande diagonale du cube ( schéma ci-dessus)

a racine carrée (3) = 4 R soit a = 4 *3-½ R

V= a3 = ( 4 *3-½ R)3 .

 La masse volumique r (kg m-3) est la masse d'une maille (kg) divisée par le volume de la maille (m3)

r =m /V = 2MTi / [ NA( 4 *3-½ R)3 ]

( 4 *3-½ R)3 = r NA/(2MTi)

R3 =33/2r NA/(2*43MTi)

R= 3½ / 4 [r NA/(2MTi)]1/3.

 
r = 4327 kg m-3 ; NA=6,02 1023 mol-1 ; MTi = 47,9 10-3 kg/mol.

R= 3½ / 4 [4327 *6,02 1023/(2* 47,9 10-3)]1/3.

R= 3½ / (4 * 3,007 109 )= 1,44 10-10 m

R= 144 pm.

 

Métallurgie du titane :

 La réduction du tétrachlorure de titane par le magnésium à 1073 K est la dernière étape de la fabrication du titane métal.

Dans cette partie on étudie cette réaction en traçant le diagramme d'Ellingham relatif aux chlorures ramené à une mole de dichlore, pour le titane et pour le magnésium, dans le domaine ; :800 K < T<1200 K.

On donne l'enthalpie libre standart DrG°1 associée à la réaction (1) valable dans le domaine de température étudié :

(1) ½Ti(s) + Cl2 (g) = ½TiCl4(g)

DrG°1= -384,7 +0,069 T ( en kJ mol-1)

Interpréter le signe de chacun des deux termes de DrG°1, après avoir précisé ce que chaque terme représente.

DrG°1=DrH°1 - T DrS°1

On identifie la variation d'enthalpie à - 384,7 : le signe négatif indique une réaction exothermique.

On identifie la variation d'entropie à -0,069 : le signe négatif indique une évolution du système vers un ordre plus important.

( disparition d'une mole de dichlore)

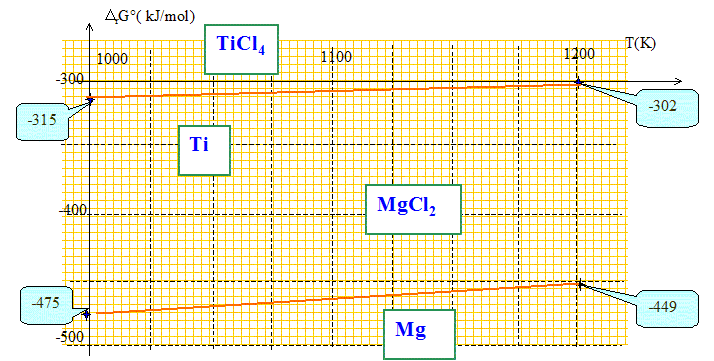
On considère la réaction (2) : Mg(l) + Cl2(g) = MgCl2 (l) DrG°2. 

Donner l'expression de DrG°2 en fonction de la température T.
Mg(l)
MgCl2 (l)
Cl2(g)
DrH° (kJ /mol)
9,2
-598,5
0
S° J K-1 mol-1
42,7
133,6
223,0
DrH°2 = DrH°(MgCl2 ) -DrH°(Cl2 )-DrH°(Mg )

DrH°2 = -598,5-9,2 = -607,7 kJ/mol.

DrS°2 =S°(MgCl2 ) -S°(Cl2 )-S°(Mg )

DrS°2 = 133,6-223-42,7 = -0,132 kJ K-1mol-1.  

DrG°2 = DrH°2 - TDrS°2.

DrG°2 = -607,7 + 0,132 T.

Tracer sur la même feuille DrG°1 = f1(T) et DrG°2 = f2(T) si 1000 K < T<1200 K.

 

 

Déduire du diagramme l'équation de la réaction qui se produite entre 1000 K et 1200 K.

 Le magnésium réduit TiCl4 suivant :

2Mg +  TiCl4 = Ti + 2MgCl2.

Calculer l'enthalpie libre standard DrG de cette réaction à 1073 K.

DrG = DrG°2 -DrG°1

DrG = (-607,7 + 0,132 T) - (-384,7 +0,069 T)

DrG =  -223 + 0,063 T

DrG =-223 + 0,063*1073 = -155 kJ / mol.

Le titane en solution aqueuse : diagramme potentiel-pH :

On se propose de déterminer les domaines de corrosion, passivation et immunité à partir du diagramme potentiel-pH donné. Ce diagramme est tracé pour une concentration en chaque espèce dissoute égale à 10-6 mol/L.

On donne :

Ti2+ + 2HO- = TiO(s) + H2O ; K1 = 1017.

2Ti3+ + 6HO- = Ti2O3(s) + 3H2O ; K21 = 1099.

Exprimer les constantes K1 et K2 en fonction des concentrations.

K1 = 1 / ( [Ti2+][HO-]2).

K2 = 1 / ( [Ti3+]2[HO-]6).

Calculer le pH limite d'existence de l'oxyde TiO(s).

[HO-]2 = 1 / ( [Ti2+] K1) = 1/(10-6 * 1017) =10-11 ;

[HO-] = 10-5,5 ; [H3O+]= 10-14 / 10-5,5 = 10-8,5 d'où pH= 8,5.

Calculer le pH limite d'existence de l'oxyde Ti2O3(s).

[HO-]6 = 1 / ( [Ti3+] K2) = 1/(10-12 * 1099) =10-87 ;

[HO-] = 10-14,5 ; [H3O+]= 10-14 / 10-14,5 = 100,5 d'où pH= -0,5.

Dans le domaine 0< pH <14, on ne considère pas l'existence de l'ion Ti3+.

Déterminer le nombre d'oxydation de l'élément titane dans les espèces suivantes :

Ti2+ : +II ; Ti : 0 ; TiO : +II ; TiO2 : +IV ; Ti2O3 : +III.

Placer ces espèces dans le diagramme donné.

Quelle espèce se dismute ?

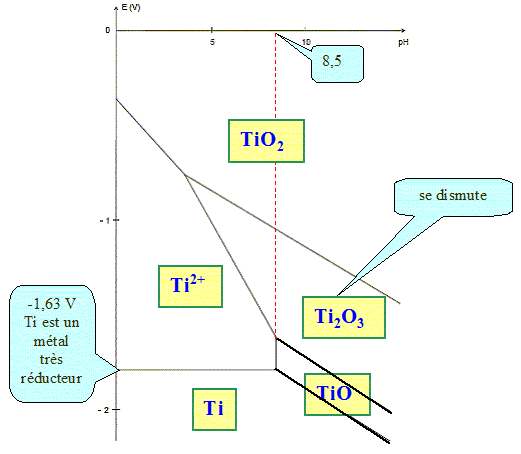
Le titane est un métal très réducteur. Pourtant il est utilisé dans les alliages pour sa résistance à la corrosion.

Expliquer cette apparente contradiction.

Une couche protectrice passivante de quelques micromètres d'épaisseur, constituée majoritairement d’oxyde TiO2, recouvre le métal.

Cette couche est très stable sur un large domaine de pH et de température.

retour -menu