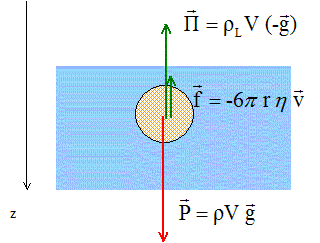Aurélie 04/10/07
 

Sédimentation : décantation et centrifugation BTS bioanalyses et contrôles 2007

En poursuivant votre navigation sur ce site, vous acceptez l’utilisation de Cookies vous proposant des publicités adaptés à vos centres d’intérêts.

. .
.
.

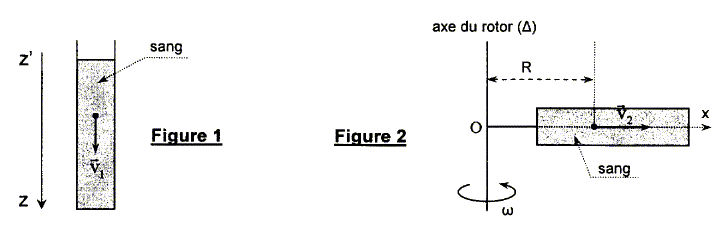
Les vecteurs sont écrits en gras et en bleu.

L'émoglobine est un pigment de coloration rouge contenu dans les globules rouges ( hématies) qui permet le transport de l'oxygène des poumons vers les tissus. C'est une protéine géante. Elle peut être modélisée par une sphère de diamètre d'environ 10 nm.

On se propose d'étudier la sédimentation de l'hémoglobine contenue dans le sang par décantation puis par centrifugation.

Dans les deux cas, les molécules d'hémogloine sont considérées comme sphériques et elles migrent dans les sens indiqués par les vecteurs vitesses v1 et v2.

On notera r, le rayon de la molécule, r sa masse volumique, rL celle du liquide, g l'accélération de la pesanteur et a l'accélération due à la rotation.

Données :

masse volumique du sang : rL =1,05 103 kg m-3

masse volumique de l'hémoglobine à la température de travail r =1,35 103 kg m-3

viscosité du sang à la température de travail h =4,0 10-3 Pa s ; g = 9,81 m s-2.

volume d'une sphère V= 4/3p r3 ; rayon de la molécule d'hémoglobine r =5,00 10-9 m

Loi de Stokes : la force de frottement sur une particule sphérique de rayon r en mouvement dans un liquide de viscosité h s'écrit f = - 6prh v.

La poussée d'Archimède correspond au poids de liquide déplacé.

Séparation de l'hémoglobine par décantation ( sous l'action de la pesanteur)

Donner l'expression des forces qui s'exercent sur cette molécule en fonction des donnes et les représenter sur un schéma.

Le mouvement de la molécule devient rapidement rectiligne uniforme.

Appliquer le principe d'inertie et retrover l'expression de la vitesse de migration v1 de la molécule donnée par :

v1 =2r2(r-rL)g /(9h)

Dans un mouvement rectiligne uniforme, les forces appliquées à la molécule se neutralisent :

rVg = rLVg + 6prhv1 ; 6prhv1 =Vg (r-rL)

avec V= 4/3p r3

6prhv1 =4/3p r3 g (r-rL) ; 3hv1 =2/3 r2 g (r-rL) ;

v1 =2r2(r-rL)g /(9h)

Calculer v1.

v1 = 2*(5,00 10-9)2(1,35 103 -1,05 103)*9,81 / (9*4,0 10-3 )

v1 = 4,1 10-12 m/s.

Quelle serait la durée t1 ( en secondes puis en années) nécesaire pour que la molécule sédimente sur une distance de 1 mm ?

d= 10-3 m ; v1 = 4,1 10-12 m/s ; t1 = d/ v1 =10-3 /4,1 10-12 ; t1=2,4 108 s = 7,7 ans.

Séparation de l'hémoglobine du sang par centrifugation :
La molécule est soumise à l'accélération a = w2R due au mouvement de rotation imprimé au tube par le rotor de la centrifugeuse ( w vitesse de rotation du rotor en rad/s et R la distance entre la molécule et l'axe du rotor )

R= 6 cm ; w =1,57 103 rad/s.

Calculer l'accélération a.

a = w2R = (1,57 103)2* 0,06 = 1,48 105 m/s2.

Calculer le rapport a/g.

1,48 105 /9,81 = 1,51 104.

La vitesse de migration de la molécule vers le fond du tube atteint rapidement une valeur constante v2 =2r2(r-rL)a /(9h)

Calculer v2.

v2 = 2*(5,00 10-9)2(1,35 103 -1,05 103)*1,48 105 / (9*4,0 10-3 )

v1 = 6,17 10-8 m/s.
Quelle serait la durée t2 ( en secondes puis en heures) nécesaire pour que la molécule sédimente sur une distance de 1 mm ?

d= 10-3 m ; v2 = 6,17 10-8 m/s ; t2 = d/ v2 =10-3 /6,17 10-8 ; t2=1,62 104 s =4,5 heures.
retour -menu