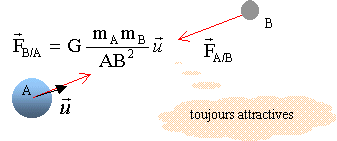|
Satellites d'observation bac Amérique du sud 2007 En poursuivant votre navigation sur ce site, vous acceptez l’utilisation de Cookies vous proposant des publicités adaptés à vos centres d’intérêts. |
||||||
|
||||||
|
ENVISAT : un satellite circumpolaire. C'était le plus gros satellite européen d'observation lors de son lancement le 1er mars 2002. Ses capteurs peuvent recueillir des données à l'intérieur d'une bande de largeur au sol de 3000 km permettant une observation biquotidienne de l'ensemble de la planète. Données : constante de gravitation universelle : G = 6,67 10 -11 SI ; ENVISAT : masse : m = 8200 kg altitude moyenne : h = 800 km ; orbite contenue dans un plan passant par les pôles TERRE : masse : M = 5,98 1024 kg ; rayon : R = 6,38 103 km ; période de rotation propre : 1436 minutes On rappelle l'expression de la valeur de la force d'interaction gravitationnelle entre deux corps de masse mA et mB , de centres A et B, de répartition de masse à symétrie sphérique, distants de d = AB : F = GmAmB / AB2. Représenter la force d'interaction gravitationnelle exercée par la Terre (sa répartition de masse étant supposée à symétrie sphérique) sur le satellite supposé ponctuel et noté B. Donner l'expression vectorielle de cette force en représentant le vecteur unitaire choisi :
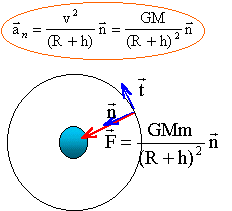
Calculer la valeur de cette force. AB = R+h = 6,38 103 + 800 = 7180 km = 7,18 106 m. F= 6,67 10 -11 *5,98 1024*8200 / (7,18 106)2 =6,34 104 N. En considérant la seule action de la Terre, établir l'expression vectorielle de l'accélération du satellite dans le référentiel géocentrique, supposé galiléen, en fonction de M, h et R. Le satellite est soumis à la seule force de gravitation centripète exercée par la planète
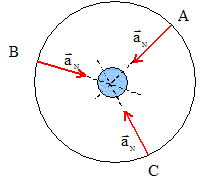
M : masse (kg) de la planète ; m : masse du satellite (kg) ; R (m) rayon planète ; h (m) altitude depuis le sol Représenter, sans souci d'échelle, le vecteur accélération à trois dates différentes correspondant aux positions A, B et C du satellite.
Montrer que, dans le cas d'un mouvement circulaire, dont on admettra sans démonstration qu'il est uniforme, la vitesse du satellite a pour expression : v = [GM / (R+h)]½. Suivant l'axe n la seconde loi de Newton s'écrit : GMm /(R+h)² = m aN Or aN =v²/ (R+h) d'où GMm /(R+h)² = mv²/ (R+h) Valeur de la vitesse (m/s): v² =GM / (R+h). v = [GM / (R+h)]½. Calculer la vitesse du satellite en km.s-1. v = [6,67 10 -11 *5,98 1024 / 7,18 106]½ =7,4533 103 m/s = 7,45 km/s. Donner l'expression de la période de révolution du satellite en fonction de sa vitesse et des caractéristiques de la trajectoire R et h. La période de révolution T du satellite (seconde) est le temps mis par le satellite pour faire un tour et ce d'un mouvement uniforme. 2 p (R+h) =vT élever au carré, puis remplacer v² par l'expression ci dessus. 4p² (R+h) ² = v² T² = GM/ (R+h) T² ou T² =4p² /(GM)(R+h)3. soit T² /(R+h)3 = 4p² / (GM) rapport constant pour une planète donnée.(3ème loi de Kepler) distance en mètre, période en seconde, masse en kg. T = 2p (R+h)3/2 / (GM)½. Calculer sa valeur. T2 = 4*3,142 *(7,18 106)3 / (6,67 10 -11 *5,98 1024 ) =3,6635 107 s2. T =(3,6635 107 )½= 6,05 103 s.
METEOSAT 8 : un satellite géostationnaire. Ce satellite a été lancé par ARIANE 5 le 28 août 2002. Il est opérationnel depuis le 28 janvier 2004. La position d'un satellite géostationnaire parait fixe aux yeux d'un observateur terrestre. Situé à une altitude H voisine de 36000 km, il fournit de façon continue des informations couvrant une zone circulaire représentant environ 42% de la surface de la Terre. Donner les trois conditions à remplir par METEOSAT 8 pour qu'il soit géostationnaire. - L'orbite est dans le plan équatorial de la terre. - Le satellite tourne dans le même sens que la terre. - Le satellite et la terre ont la même vitesse angulaire. Troisième loi de Kepler dans le cas général d'une trajectoire elliptique : Pour tous les satellites, le rapport entre le carré de la période de révolution T et le cube du demi-grand axe r de sa trajectoire est le même : T2/r3 = constante = K. Dans le cas d'une trajectoire circulaire r correspond au rayon de la trajectoire. En utilisant les réponses aux questions précédentes, établir l'expression de la constante K en fonction de G et M pour les satellites étudiés. La période de révolution T du satellite (seconde) est le temps mis par le satellite pour faire un tour et ce d'un mouvement uniforme. 2 p (R+h) =vT élever au carré, puis remplacer v² par l'expression ci dessus. 4p² (R+h) ² = v² T² = GM/ (R+h) T² ou T² =4p² /(GM)(R+h)3. soit T² /(R+h)3 = 4p² / (GM) rapport constant pour une planète donnée.(3ème loi de Kepler) Calculer K dans le système international d'unités. K = 4*3,142/ (6,67 10 -11 *5,98 1024 )=9,90 10-14 SI. En déduire, pour METEOSAT 8, la valeur de R+h, puis celle de h. T= 1436 min = 1436*60 = 8,616 104 s ; T2 =7,4235 109 s2. (R+h)3 = T² /K =7,4235 109 / 9,90 10-14 =7,498 1022 R+h =4,22 107 m = 4,22 104 km. h = 4,22 104-6,38 103 = 3,58 104 km.
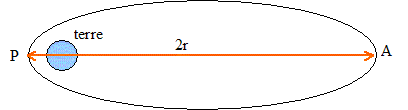
La mise en place du satellite sur l'orbite géostationnaire s'effectue en plusieurs étapes. Tout d'abord, ARIANE 5 amène le satellite hors de l'atmosphère et le largue sur une orbite de transfert. L'orbite de transfert parcourue par le satellite est une ellipse dont le périgée P se situe à une altitude voisine de 200 km et l'apogée A à l'altitude de l'orbite géostationnaire voisine de 36000 km. Ensuite le " moteur d'apogée " du satellite lui permettra d'obtenir la vitesse nécessaire à sa mise sur orbite géostationnaire lors des passages successifs par l'apogée.
A l'aide des données ci-dessus, calculer la longueur r du demi-grand axe de la trajectoire sur cette orbite de transfert. 2 r = R+200 + R +36000 = 2R+36200 r = R+18100 = 6380+18100 = 2,448 104 km = 2,45 104 km. A l'aide de la troisième loi de Képler, en déduire la période T du satellite sur cette orbite de transfert. T²=K(R+h)3 = K r3 = 9,90 10-14 *(2,448 107)3 =1,32 109 T=(1,32 109)½ = 3,63 104 s.
|
||||||
|
|
||||||
|
|