Aurélie 20/08/07
 

Etude d'un dipole inconnu : oscillogramme ; construction de Fresnel bac STL chimie de laboratoire, procédés industriels 2007 France

 
. .

Google


 

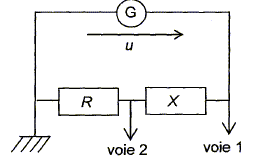
On souhaite déterminer la nature et la valeur de la grandeur caractéristique d'un dipole inconnu noté X. Pour cela, on réalise le montage ci-dessous :

Ce circuit comporte en série :
- un générateur G délivrant une tension sinusoïdale u(t) de fréquence f= 50 Hz

- un conducteur ohmique de résistance R= 75 W

- le dipole inconnu qui peut être soit un conducteur ohmique de résistance Rx, soit une bobine supposée parfaite d'inductance L, soit un condensateur de capacité C.

Un oscilloscope bicourbe, branché comme indiqué sur la figure, permet d'observer l'oscillogramme suivant :

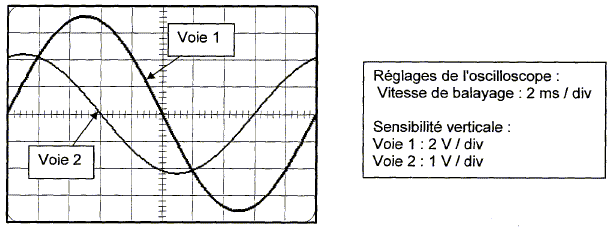
Etude de l'oscillogramme :

  1. Que visualise t-on sur chaque voie ?
  2. Quel est l'intérêt de visualiser la tension sur la voie 2 ?
  3. Déterminer les valeurs maximales des tensions u(t) et uR(t) ; en déduire les valeurs efficaces correspondantes.
  4. Calculer la valeur efficace de l'intensité i(t) du courant dans le circuit.
  5. Déterminer le déphasage de la tension u(t) par rapport à l'intensité i(t). Justifier son signe.
  6. En déduire la nature du dipole inconnu X.
  7. Calculer l'impédance du dipole R-X constitué par l'association en série du conducteur ohmique et du dipole X. En déduire la grandeur caractéristique du dipole X.
Réponse : 

 Sur la voie 1 on visualise u(t), tension aux bornes du générateur ou la tension aux bornes du dipole R-X.

Sur la voie 2 on visualise uR(t), tension aux bornes du conducteur ohmique. Or l'intensité i(t) et la tenion uR(t) sont proportionnelles : uR(t) est donc l'image de i(t) au facteur R près.

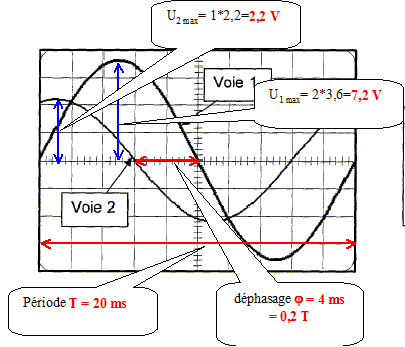
Valeurs efficace de la tension u(t) : U= 7,2 / 2½ = 5,1 V ; valeurs efficace de la tension uR(t) : UR= 2,2 / 2½ = 1,6 V

Valeur efficace de l'intensité : I = UR/ R = 1,6/75=2,1 10-2 A.

Déphasage de la tension u(t) par rapport à l'intensité i(t).  

La courbe uR(t) passe la première par un maximum ; uR(t) est en avance sur u(t) : l'intensité i(t) est en avance sur u(t) ; u(t) est en retard sur i(t) de :

j = -0,2 T; or T= 2p radians d'où j =-0,4p radians. (-72° )

Le dipole X est donc un condensateur.

impédance du dipole R-X :

Z = U/I = 5,1/2,1 10-2 = 243 W.

impédance complexe Z = R- j/ (Cw) avec w = 2pf = 100 p = 314 rad/s.

Z2 =[R2 + 1/(Cw)2] ; 1/(Cw)2 =Z2 - R2 = 2432-752 = 5,34 104 ;

1/(Cw) = 231 W ; C = 1/(231*314) = 1,4 10-5 F.
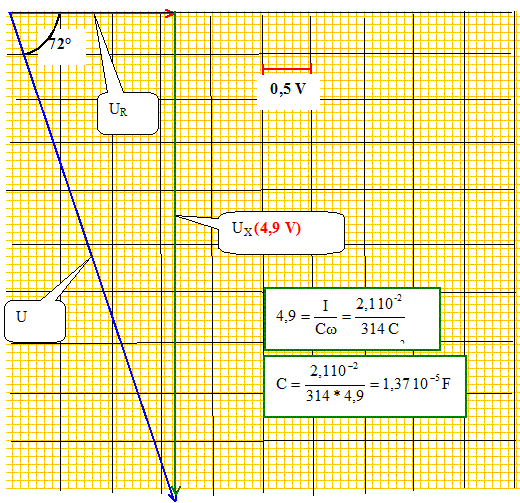
Construction de Fresnel :

 On se propose de retrouver cette valeur à l'aide d'une construction de Fresnel.

  1. Tracer les vecteurs de Fresnel associés à u(t) et uR(t) à l'aide des valeurs efficaces et du déphasage.
  2. En utilisant la loi des mailles, donner l'expression de la tension uX(t) aux bornes du dipole inconnu en fonction de u(t) et uR(t). En déduire la construction du vecteur de Fresnel associé à uX(t).
  3. Mesurer précisément la valeur efficace de uX(t). Retrouver la valeur de la grandeur caractéristique du dipole inconnu.
 

Réponse : 

La phase de uR(t) est choisie comme origine des phase ; u(t) présente un déphasage de -72°.

Valeurs efficaces : U= 5,1 V ; UR = 1,6 V

loi des mailles : u(t) = uX(t)+ uR(t) ; uX(t) = u(t)- uR(t)

 

 
retour -menu