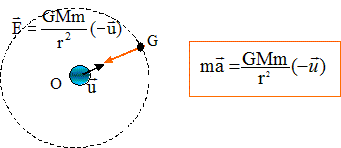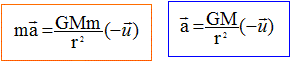|
bac
S Polynésie
2007 : gravitation,
satellite, 3ème loi de Kepler. En poursuivant votre navigation sur ce site, vous acceptez l’utilisation de Cookies vous proposant des publicités adaptés à vos centres d’intérêts. |
|||||||||||||||||||||||||||||||||||||||||||||||||||
|
|||||||||||||||||||||||||||||||||||||||||||||||||||
|
GALILEO repose sur une constellation de 30 satellites et des stations terrestres permettant de fournir des informations concernant le positionnement à des usagers de nombreux secteurs ( transport, services sociaux, justice…) Le premier satellite du programme, Giove-A, a été lancé le 28 /12 /2005. D'après le site http://www.cnes.fr Données : G = 6,67 10-11 m3 kg-1 s-2 La terre est supposée sphérique et homogène. On appelle O son centre, sa masse M=5,98 1024 kg et son rayon R= 6,38 103 km. Le satellite Giove-A est assimilé à un point matériel G de masse m = 700 kg. Il est supposé soumis à la seule force gravitationnelle due à la terre, et il décrit de façon uniforme un cercle de centre O, à l'altitude h=23,6 103 km. Mouvement du satellite Giove-A autour de la terre : Sans souci d'échelle, faire un schéma représentant la terre, le satellite sur sa trajectoire et la force exercée par la terre sur le satellite. En utilisant les notations du texte, donner l'expression vectorielle de cette force. On notera u le vecteur unitaire dirigé de O vers G.
Dans quel référentiel le mouvement du satellite est-il décrit ? Quelle hypothèse concernant ce référentiel faut-il faire pour appliquer la seconde loi de Newton ? En appliquant la seconde loi de Newton au satellite, déterminer l'expression du vecteur accélération a du point G.
Donner les caractéristiques du vecteur accélération d'un point matériel ayant un mouvement circulaire uniforme. Montrer que la vitesse du satellite est telle que : v2 = GM/r avec r = R+h Définir la période de révolution du satellite. Donner son expression en fonction de G, M et r. Calculer la période T. Schéma représentant la terre, le satellite sur sa trajectoire et la force exercée par la terre sur le satellite. On note r = R +h.
Référentiel d'étude du mouvement du satellite : géocentrique. L'origine du repère est le centre de la terre. Ce référentiel est supposé galiléen : dans un tel référentiel les lois de Newton s'appliquent. Expression du vecteur accélération a du point G.
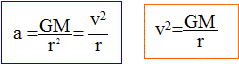
Caractéristiques du vecteur accélération d'un point matériel ayant un mouvement circulaire uniforme : Ce vecteur est appliqué au point G ; il est dirigé de G vers O : on dit que l'accélération est centripète. La valeur de l'accélération s'exprime par : a = v2/r. v : vitesse en m/s et r (m) rayon de l'orbite circulaire.
Vitesse du satellite :
Période de révolution T du satellite. Durée (s) nécessaire pour décrire une circonférence ( 2pr en mètre) à la vitesse v ( m/s) définie ci-dessus. 2pr = v T ; T= 2pr / v. Expression de T en fonction de G, M et r : Elever au carré l'expression de la période : T2 = 4p2 r 2 / v2. Remplacer v2 par son expression GM/ r : T2 = 4p2 r 3 / (GM). T = 2p[r 3 / (GM)]½. Calcul de la période T : r = (6,38 + 23,6 ) 106 = 3,0 10 7 mètres. r 3=2,7 1022 m3 ; r 3/(GM) =2,7 1022 /(6,67 10-11 * 5,98 1024) =6,75 107 s2. [r 3 / (GM)]½=8,22 103 s ; T= 6,28 *8,22 103 = 5,16 104 s.
Le tableau suivant rassemble les
périodes T et les rayons r des trajectoires des
satellites correspondants, ainsi que les données
relatives aux satellites de type
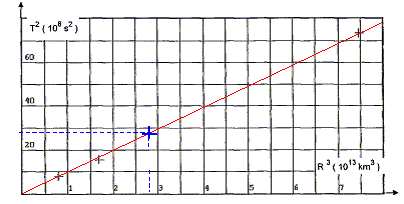
Météosat. Ces données permettent de tracer la courbe donnant T2 en fonction de R3.
Point correspondant dans le système d'axes proposés et courbe donnant T2 en fonction de R3.
La droite passant par l'origine indique que le carré de la période T2 et le rayon au cube de l'orbite r3 sont des grandeurs proportionnelles. Le résultat précédent T2 = 4p2 r 3 / (GM), dans lequel 4p2/ (GM) est une constante ( pour un astre central donné), est conforme au tracé obtenu. La loi ainsi mise en évidence est la 3ème loi de Kepler.
|
|||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||
|
|