|
Donnée : c = 3,00 108 m/s.
En astronomie on cherche à observer les ondes
électromagnétiques qui nous parviennent des
étoiles. La lumière n'est qu'une petite partie
du spectre étudié.
- Les ondes électromagnétiques couvre
l'ensemble du spectre émis depuis plus de 1 km de
longueur d'ondes jusquà quelques
nanomètres. Donner la relation entre la longueur
d'onde l, la
célérité c et la fréquence de
l'onde N.
- Ordonner qualitativement les différents
domaines des ondes électromagnétiques (
radio, ultraviolet UV, infrarouge ( IR), X, visible et
gamma en fonction de leur longueur d'onde.
- Les radioastronomes s'interessent par exemple
à la fréquence de 470 MHz. Calculer la
longueur d'onde correspondante. Dans quel domaine ce
rayonnement se situe t-il ?
- Le télescope du Mont Palomar est de type
Newton : la lumière réfléchie par le
miroir principal est ensuite réfléchie par
un miroir secondaire. Le miroir principal est parabolique
mais nous ferons l'approximation qu'il s'agit d'un miroir
sphérique, de diamètre D= 5,08 m, de
distance focale f= 16,3 m. Le miroir secondaire est
plan.
- La lumière provenant d'un astre situé
à l'infini entre dans le télescope
parallèlement à l'axe optique de celui-ci.
Où se formerait l'image A de l'astre en absence de
miroir secondaire ? Faire le schéma
correspondant.
- Le miroir secondaire est situé à d = 14 m
du sommet du miroir principal, et incliné de
45° sur l'axe optique de celui-ci. Quelle est la
position de l'image A' de A donnée par ce miroir
?
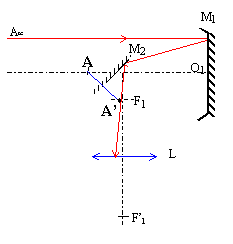
- Faire le schéma à l'échelle (
1/100) le schéma du parcours d'un rayon lumineux
qui entre dans le télescope parallélement
à l'axe. Préciser ce qui se passe
après réflexion sur le miroir principal,
après réflexion sur le miroir
secondaire.
- On veut observer cette image A' à l'aide d'une
lentille oculaire(L) de distance focale f'= 0,50 m.
Comment faut-il placer cette lentille de manière
à ce que l'image définitive A" se forme
à l'infini ? Préciser la position de (L)
sur le schéma.
- Limites :
Une qualité recherchée pour un instrument
d'optique est sa capacité à distinguer deux
détails voisins, par exemple, séparer
uneétoile double, voir un cratère lunaire
de petite dimension. Les lois de l'optique
géométriques font que deux points distincts
A et B donnent deux images séparées. Mais
différents phénomènes ( dont la
diffraction des ondes) entraînent que l'observateur
O ne peut discerner deux images distinctes que si l'angle
AOB est supérieur à l'angle a
appelé limite de résolution.
A et B donnent pour l'observateur placé en O deux
images distinctes :
On montre que pour des points à l'infini et un
instrument dont le diamètre de l'objectif est D,
la limite de résolution, exprimée en
radians, pour une lumière de longueur d'onde
l, vaut a
= 1,22 l
/D.
- Calculer la limite de résolution a1
de l'oeil humain nu pour une lumière de longueur
d'onde l=600 nm, sachant que
la pupille a un diamètre de 2,5 mm.
- Calculer la limite a2
de résolution du télescope
du Mont Palomar pour la même longueur d'onde.
- Pour observer les autres domaines spectraux que le
visible, et notammùent aux grandes longueurs
d'onde, on a construit sur le même principe des
radiotélescopes.
- Dans le cratère météoritique,
à Arecibo dans l'ile de Porto Rico, le grand
radiotélescope possède un réflecteur
( miroir principal) parabolique de 305 m. Calculer la
limite a3 de
résolution de ce radiotélescope pour la
radiation électromagnétique de
fréquence 470 MHz. Comparer avec le
résultat obtenu pour le télescope du Mont
Palomar.
Relation entre la longueur d'onde l,
la célérité c et la fréquence de
l'onde N :
l
= c/N.

Longueur d'onde correspondante à N= 470 MHz
= 4,7 108 Hz.
l
= c/N = 3 108 / 4,7 108 =
0,64 m. ( domaine des
ondes radio)
Le télescope de type Newton
:
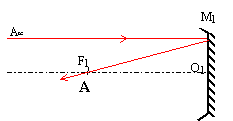
L'image de l'astre situé à
l'infini se forme au foyer du miroir
sphérique.
|
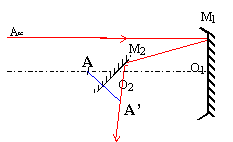
A' est symétrique de A par rapport au
plan du miroir.
|
L'image définitive A" se forme à l'infini si
l'objet A' se trouve dans le plan focal objet de la lentille
(L).
Limite de résolution a1
de l'oeil humain nu pour une lumière de longueur
d'onde l=600 nm = 6
10-7 m, sachant que la pupille a un
diamètre D=2,5 mm = 2,5 10-3 m.
a1 = 1,22
l /D = 1,22* 6
10-7 /2,5 10-3 =
2,9 10-4
rad.
Limite a2 de
résolution du télescope du Mont Palomar pour
la même longueur d'onde ; D = 5,08 m
a2 = 1,22
l /D = 1,22* 6
10-7 /5,08 = 1,44
10-7 rad.
Limite a3
de résolution de ce
radiotélescope pour la radiation
électromagnétique de fréquence 470 MHz
:
D= 305 m ; l = 0,64 m ;
a3 = 1,22
l /D = 1,22*
0,64 /305 = 2,6 10-3
rad.
( environ 20 000 fois a2
limite de résolution du
télescope du Mont Palomar)
|