Aurélie 27/06/07
 

notice d'un télescope, cerle oculaire, diamètre apparent bacS 2007 Antilles
. .

Google


4 points ; d'autres corrigés labolycée.org ; intellego.fr ; montblancsciences.free.fr.

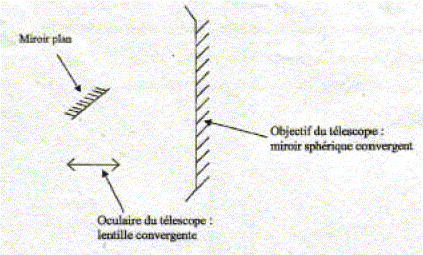
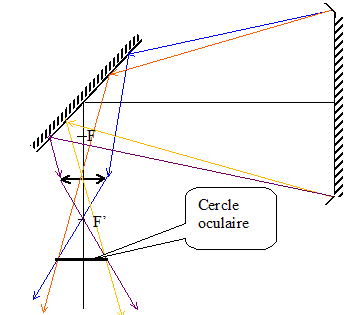
Diamètre de l'objectif : D1 = 114 mm ; distance focale de l'objectif f'1 = 1000 mm ; rapport f'1/D1 : 8,8

Accessoires fournis : Oculaire MA 25 distance focale f'2 = 25 mm (40 fois)

Oculaire MA 9 distance focale f'3 = 9 mm (111 fois)

Diamètre des oculaires : D2 = D3 = 31,75 mm ; chercheur : 6x30 ; grossissement maximum utile : 228 fois

Plus petit détail visible sur la Lune : 2,1 km.

On rappelle le schéma de principe du télescope.

Constitution du télescope :
Les distances algébriques sont écrites en gras et en bleu.

  1. L'objectif du télescope est un miroir sphérique convergent.
    À l'aide des données et en utilisant les échelles, placer sur le schéma ci-dessous, le sommet S du miroir sphérique convergent ainsi que son foyer principal F. On appelle le centre du miroir C.
    - Quelle relation existe-t-il entre CS et CF ?
    - Où se forme l'image d'un objet placé à l'infini ?
    - Construire sur le schéma ci-dessous l'image d'un objet lumineux situé à l'infini (étoile). Un des rayons issu de l'objet est représenté sur le document.
    Échelle suivant l'axe optique 1/10. Échelle perpendiculairement à l'axe optique 1/2.
  2. Le miroir sphérique donne une image intermédiaire qui est réfléchie par le miroir plan. On obtient ainsi une deuxième image intermédiaire qui constitue un objet pour l'oculaire.
    - On veut obtenir une image finale à l'infini. Où cette deuxième image intermédiaire doit-elle se former par rapport à l'oculaire ?
    -Vérifier votre affirmation avec l'aide de la formule de conjugaison.
  3. Etude du cercle oculaire.
    - Définir le cercle oculaire.
    - Positionner le cercle oculaire sur le schéma ci-dessous.
    - Indiquer son intérêt pratique.
Relation entre CS et CF :

CS = 2CF ( F est à égale distance de C et S)

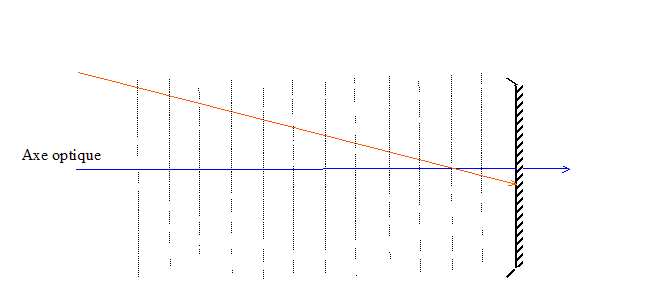
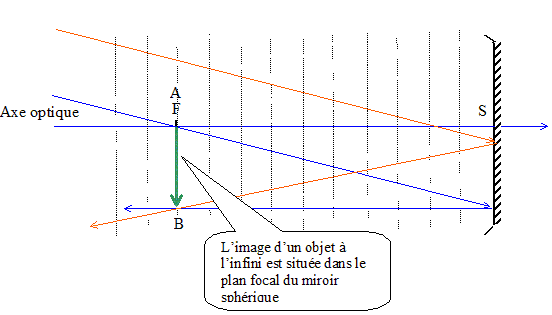
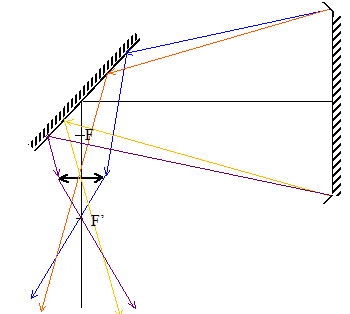
 Le miroir sphérique donne une image intermédiaire qui est réfléchie par le miroir plan. On obtient ainsi une deuxième image intermédiaire qui constitue un objet pour l'oculaire.
On veut obtenir une image finale à l'infini :

cette deuxième image intermédiaire doit se former dans le plan focal objet de l'oculaire.
En effet la formule de conjugaison, pour une lentille convergente, l'oculaire, s'écrit :

1/f' = 1/OA'-1/OA. ( O : centre optique de l'oculaire, A : objet , A' : image de A donnée par l'oculaire)

si OA= - f' alors 1/OA'= 0 et OA' tend vers l'infini.

Le cercle oculaire :

c'est l'image de l'objectif ( ici miroir convergent + miroir plan), donnée par l'oculaire.


Son intérêt pratique :

Toute la lumière issue du télescope passe par le cercle oculaire : en plaçant l'oeil à cet endroit, l'image définitive observée est très lumineuse.

 
Grossissement du télescope :

Sachant que le grossissement G du télescope est donné par la relation :

G = distance focale de l'objectif / distance focale de l'oculaire.

  1. Lequel des deux oculaires fournis faut-il choisir pour avoir le plus grand grossissement ? Justifier la réponse.
    On précise que le grossissement maximum utile est le grossissement maximal possible compte tenu du diamètre de l'objectif. On peut obtenir ce grossissement maximal possible avec un oculaire non fourni.
  2. Calculer la distance focale de l'oculaire nécessaire pour obtenir le grossissement maximum utile de 228 fois.
  3. Le grossissement du télescope peut s'écrire :
    G = diamètre apparent de l'objet à travers le télescope / diamètre apparent de l'objet = q '/q.
    - Rappeler la définition du diamètre apparent q.
    -Calculer le diamètre apparent q (en radian) du plus petit détail visible sur la Lune (2,1 km) sachant que la distance Terre-Lune sera estimée à 3,8.105 km.
    - Calculer le diamètre apparent q ' de l'objet à travers le télescope si on utilise l'oculaire de distance focale f'3 = 9 mm. 
G = distance focale de l'objectif / distance focale de l'oculaire.

Pour une distance focale de l'objectif constante, le grossissement est d'autant plus grand que la distance focale de l'oculaire est plus petite.

Choisir l'oculaire : Oculaire MA 9 distance focale f'3 = 9 mm (111 fois).

Distance focale de l'oculaire nécessaire pour obtenir le grossissement maximum utile de 228 fois :

G = f'1 / f' oculaire ; f' oculaire = f'1 /G = 1000 / 228 = 4,39 mm.

Diamètre apparent q :

tan q = dimension de l'objet / distance de l'objet à l'oeil de l'observateur

Si l'objet est de très petites dimensions, ou si l'objet est très grand mais suffisamment éloigné de l'observateur, l'angle q est petit : on peut confondre la tangente et la mesure de l'angle en radian.

Les deux distances s'expriment soit en m, soit en km.

Diamètre apparent q (en radian) du plus petit détail visible sur la Lune :

q = 2,1 / 3,8 105 = 5,5 10-6 rad.

Diamètre apparent q ' de l'objet à travers le télescope si on utilise l'oculaire de distance focale f'3 = 9 mm : 

Le grossissement vaut : G= f'1 / f'3=1000/9.

De plus G= q '/q soit q '= G q avec q= 2,1 / 3,8 105

q '= 1000 * 2,1 / (9*3,8 105 ) ; q '= 6 10-4 rad.

 

 
retour -menu