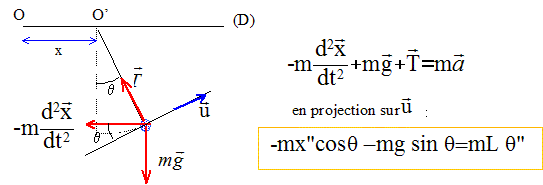Aurélie 02/06

 

Pendule excité : force d'inertie ( concours Enac )

En poursuivant votre navigation sur ce site, vous acceptez l’utilisation de Cookies vous proposant des publicités adaptées à vos centres d’intérêts.

 

. .

.
.


 

 Un pendule de longueur L est attaché à un point O' fixe. Soit g =9,8 m/s² l’accélération de la pesanteur ; on pose w0=(g/L)½.

  1. Calculer L sachant que la période des oscillations vaut T= 1s
  2. O' se déplace maintenant sur une droite horizontale. L’abscisse de O' sur la droite est nulle si le pendule est vertical ; si , t>0, l’abscisse de O' sur la droite vaut : x= xm(1-cos(wt)) . Montrer que si t>0, l’angle q formé par le pendule avec la verticale obéit à : q" + w02 sin q = -xm w2/L cosq cos (wt).
  3. Déterminer q en supposant que cet angle reste petit.
  4. On donne ci-dessous le graphe de cos(2pt)-cos(5/6 2pt). Comment est le graphe de q(t) si w/w0=5/6 en supposant que q reste petit ? Quelle condition qualitative doit vérifier xm pour qu’il soit correct ? Expliquer pourquoi le pendule semble s’arrêter périodiquement et justifier la période de ces arrêts.

corrigé
période T= 2p/w0= 2p(L/g)½ d'où L= T2g/(4p2) = 1*9,8 / (4*3,14²)= 0,248 m.

O est fixe. On choisit un référentiel en translation par rapport au référentiel terrestre. Dans ce référentiel, le pendule est soumis à son poids, à la tension du fil et à la force d'inertie d'entraînement. Ecrire la relation fondamentale de la dynamique :

avec x= xm(1-cos(wt) )et x" = w2xm cos(wt)

d'où : -w2xm cos(wt) cos q -g sin q = Lq"

diviser par L et remplacer g/L par w20 : -w2xm / L cos(wt) cos q -w20 sin q = q"

q" + w02 sin q = -xm w2/L cosq cos (wt).

si l'angle est petit : sin q = q et cos q = 1.

q" + w02 q = -xm w2/L cos (wt) (1)

la solution de cette équation différentielle est la somme de :

la solution générale de l'équation sans second membre q" + w02 q = 0, c'est à dire : q = A cos(w0t) + B sin (w0t)

d'une solution particulière de l'équation complète : q = C cos(wt)

Pour déterminer C, on repporte q et q " = -w2Ccos(wt) dans (1) :

-w2Ccos(wt) + w02C cos(wt) = -xm w2/L cos (wt)

d'où C= xm w2/(L(w2-w02))

La solution générale est : q = A cos(w0t) + B sin (w0t) + xm w2/(L(w2-w02))cos(wt)

Déterminer A et B par les conditions initiales : q (0)=0 et q'(0)=0 (la vitesse initiale de O' étant nulle, la vitesse initiale du solide m est nulle)

q (0)=0 donne : A+ xm w2/(L(w2-w02)) = 0 soit A = -xm w2/(L(w2-w02))

q'= -Aw0 sin(w0t) + B w0cos (w0t) - xm w3/(L(w2-w02))sin(wt)

q'(0) =-Bw0 = 0 soit B=0

q = xm w2/(L(w2-w02))[ cos(wt)- cos(w0t) ]

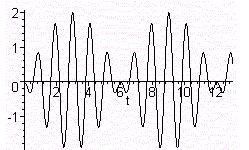
w/w0=5/6 d'où q = xm /(L(1-(6/5)2))[ cos(5/6w0t)- cos(w0t) ]

de plus w0 = (g/L)½ = (9,8/0,248)½ = 6,28 = 2 p rad/s

q = xm /(L(1-(6/5)2))[ cos(5/6 2p t)- cos(2pt) ]

le graphe de q est donc semblable à celui de cos(2pt)-cos(5/6 2pt) à un changement d'échelle verticale près.

q doit rester petit soit xm w2/(L(w2-w02)) <<1 ou bien xm<< L|(w2-w02) |/ w2

Le pendule s'arrête lorsque cos(wt)- cos(w0t) = 0 soit wt - w0t = 2kp.( k entier)

t = 2kp/ |w - w0| avec w= 5/6w0 = 5/6* 6,28 = 5,23 rad/s ; |w - w0|=6,28-5,23 = 1,05 rad/s

d'où la période des arrêts : T= 2*3,14/1,05 = 6 s.

retour -menu