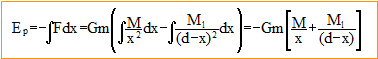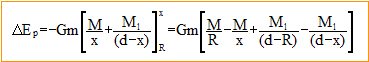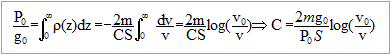th énergie cinétique, vitesse de lancement ( concours Mines 76 ) Le tir vers la Lune selon J. Verne

Aurélie 6/3/06

th. énergie cinétique, vitesse de lancement ( concours Mines 76 )

Le tir d'un obus vers la Lune selon J. Verne

En poursuivant votre navigation sur ce site, vous acceptez l’utilisation de Cookies vous proposant des publicités adaptées à vos centres d’intérêts.

. .

Vitesse de l'obus à la sortie du canon : v₀= 16,5 km/s ; L'atmosphère freine l'obus et sa vitesse devient v = 11 km/s.

A. Un mobile de masse m est animé d'un mouvement rectiligne sous l'action d'une force notée F ; on note x, son abscisse et v sa vitesse. Démontrer le théorème de l'énergie cinétique.

B. Vitesse minimale de lancement : on néglige les forces de frotements dues à l'atmosphère.

Exprimer la force de gravitation subie par un point matériel P ( de masse m) situé à la distance d=OP d'un astre à symétrie sphérique, de masse M, de centre O.
Exprimer le produit GM ( où G est la constante de gravitation) en fonction de l'accélération de la pesanteur g₀ à la surface de la Terre et du rayon R de la Terre.
Quelle est la vitesse minimale v_l de lancement pour que le projectile échappe à l'attraction terrestre ? R = 6400 km ; g₀ = 9,8 m/s²

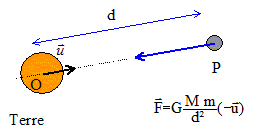
C. Vitesse de l'obus en un point quelconque : La Terre et la Lune étant immobiles dans un référentiel galiléen, l'obus (masse m) se déplace suivant la droite joignant les centres des deux astres. On note d : distance Terre Lune et x : distance Terre obus ; masse de la Lune M_l ; masse de la Terre M.

Exprimer la force de gravitation subie par l'obus .
Exprimer ½(v²-v²_l) où v est la vitesse de l'obus et v_l la vitesse minimale de lancement. Commenter cette expression.

D. Les poudres : l'obus est lancé verticalement ; la section du canon est S. Jules Verne semble estimer qu'une quantité illimitée de poudre permet d'obtenir une vitesse illimitée. Montrons que cela est faux.

A la date t, on note r₁ la masse volumique ( supposée uniforme) des gaz issus de l'explosion, gaz situés dans le canon sous l'obus. L'obus se trouve à une hauteur H au dessus du fond du canon. Donner l'expression de r₁ en fonction de H, S et de la masse m₁ de la poudre.
Exprimer la masse dm₁ des gaz situés à la distance z du fond du canon et compris dans la tranche d'épaisseur dz.
Exprimer la vitesse v₁de cette tranche de gaz ; la vitesse de l'obus est notée v. La vitesse des gaz est supposée proportionnelle à l'altitude z..
Exprimer l'énergie cinétique de l'ensemble des gaz puis de l'obus et des gaz.
Cette énergie provient de l'énergie chimique des poudres. Pour des canons utilisant les mêmes poudres avec un rendement identique. Exprimer ce rendement.
Caractéristiques du canon : masse des poudres m₁=72 kg ; masse de l'obus m = 500 kg ; vitesse initiale obus : v= 700 m/s. Si la masse de poudre était illimitée, quelle serait la vitesse de l'obus tiré par ce canon ?

E. Freinage de l'obus par l'atmosphère : La force F de freinage est du type F= ½C S r v² où C est une constante dépendant de la forme de l'obus, r la masse volumique de l'air qui dépend de l'altitude z, v la vitesse de l'obus, S section droite de l'obus.

L'atmosphère ayant une épaisseur de 10 km. Estimer la valeur de l'accélération de l'obus lors de cette traversée. Le poids de l'obus est-il négligeable ?
En utilisant le thèorème de l'énergie cinétique trouver une relation entre la variation de vitesse dv et la variation d'altitude dz.
Quelle est la masse M d'une colonne d'air de section S comprise entre le sol et une altitude infinie ? Pression atmosphérique au sol P₀ = 10⁵ Pa et g₀ = 10 m/s².
Exprimer C en fonction de la vitesse initiale v₀, de la vitesse finale v après traversée de l'atmosphère et des autres données.

corrigé

théorème de l'énergie cinétique :

différencier l'expression de l'énergie cinétique : d(½mv²) = m v dv

or la vitesse est da dérivée de l'abscisse par rapport au temps : v = dx/dt d'où : d(½mv²) = m dx/dt dv = m dv/dt dx

or m dv/dt =ma = F ( seconde loi de Newton) d'où d(½mv²) = F dx.

force de gravitation :

à la surface de la Terre : d= R et la force de gravitation est identifiée au poids P= mg₀.

vitesse minimale de lancement :

énergie potentielle E_p du point matériel de masse m situé à la surface de la Terre : E_p = -GMm/R = -g₀R² m/R= -g₀R m

énergie cinétique du point matériel de masse m et animé de la vitesse v : E_c = ½mv²

énergie mécanique : E_p +E_c = ½mv² -g₀R m/.

à l'infini : l'énergie potentielle est nulle et la vitesse est notée v_infini

énergie mécanique à l'infini : ½mv²_infini

L'énergie mécanique se conserve : ½mv²_infini= ½mv² -g₀R m.

v²_infini= v² -2g₀R.

v²_infinipositive ou nulle d'où v² -2g₀R >=0 ; v² >=2g₀R

v = racine carrée (2*9,8*6,4 10⁶) = 11200 m/s = 11,2 km/s.

On choisi un axe Ox ayant pour origine le centre de la Terre et dirigé vers la Lune.

L'obus subit la force de gravitation exercée par la Terre, dirigée vers le centre de la Terre, valeur : GMm/x²

ainsi que la force de gravitation subie par la Lune, dirigée vers le centre de la Lune, de valeur GM_lm/(d-x)²

soit F= GM_lm/(d-x)² - GMm/x²

Cette force dérive de l'énergie potentielle E_p :

La variation d'énergie cinétique ( cas de la translation) ½(v²-v²_l) est égale à l'opposée de la variation d'énergie DE_p potentielle de pesanteur :

Cette relation est fausse car le référentiel lié à la Terre et à la Lune n'est pas galiléen.( Il tourne autour du barycentre des deux astres). En conséquence l'obus ne suit pas une trajectoire rectiligne et il faut tenir compte de la force de Coriolis. De plus la distance Terre Lune n'est pas constante.

expression de r₁ en fonction de L, S et de la masse m₁ de la poudre :

masse volumique (kg m^-3) = masse (kg) / volume (m³) = r₁= m₁/(LS).

masse dm₁ des gaz situés à la distance z du fond du canon et compris dans la tranche d'épaisseur dz :

masse volumique * volume de la tranche ; dm₁ = r₁ Sdz = m₁dz/H.

vitesse v₁de ces gaz : la vitesse des gaz est supposée proportionnelle à l'altitude z.

à la distance H, la vitesse de la tranche de gaz est égale à la vitesse v de l'obus ; à la distance z : v_l = v z/H.

énergie cinétique de l'ensemble des gaz : énergie cinétique de la tranche de gaz : ½dm₁v_l²= ½m₁v²/H³ z² dz

intégrer entre 0 et H :( primitive : 1/6 m₁v²/H³z³) d'où : E_c1= 1/6 m₁v².

énergie cinétique de l'obus et des gaz : E_c= ½m v² + 1/6 m₁v².

L'énergie chimique est proportionnelle à la masse des poudres. On définit le rendement de la manière suivante :

rendement = énergie cinétique / énergie chimique = (½m + 1/6 m₁)v² / (km₁) = (½m / m₁ + 1/6 )v² / k

k constante caractéristique des poudres.

si m₁ tend vers l'infini, le rendement tend vers 1/6 v²_infini/ k

le rendement étant constant : 1/6 v²_infini = (½m / m₁ + 1/6 )v²

v²_infini =(3 m / m₁ + 1)v² = (3*500/72 +1)*700² = 1,07 10⁷ soit v_infini =3270 m/s.

valeur de l'accélération de l'obus lors de cette traversée : h : épaisseur de l'atmosphère, a : accélération lors de la traversée.

Ecrire le thèorème de l'énergie cinétique : ½mv²-½mv²₀ = mah

d'où |a|= (v²₀ - v²)/ 2h = (16,5²-11²) 10⁶ / 2 10⁴ = 7,5 10³ m/s²

valeur très supérieure à g₀ ; le poids est négligeable lors de cette traversée.

relation entre la variation de vitesse dv et la variation d'altitude dz :

la variation de l'énergie cinétique est égale au travail de la force de frottement : d(½mv²) =m v dv = -½C S r v² dz

d'où dv / v = - C S r/(2m) dz

masse M d'une colonne d'air de section S comprise entre le sol et une altitude infinie :

masse d'une tranche d'air de section S, d'épaisseur dz, située à l'altitude z : dm = rSdz

puis intégrer entre z=0 et l'infini pour obtenir M :

Cette colonne d'air est en équilibre sous l'action de son poids et des forces pressantes dues à l'air extérieur.

En haut , pression nulle, donc force pressante nulle ; en bas pression P₀, force pressante P₀S ; sur les faces verticales les forces pressantes s'équilibrent.

d'où Mg₀ = P₀S ; M/S= P₀/ g₀ et rdz = -2m/ (CS)dv / v .

retour -menu