|
Lentille divergente En
poursuivant votre navigation sur ce site, vous acceptez l’utilisation
de Cookies vous proposant des publicités adaptées à vos centres
d’intérêts. |
||
| .
. |
||
|
||
|
|
Un objet de 20 mm de taille est observé derrière une lentille de -5 dioptries ; il est placé à 15 mm de la lentille. Quelle taille aura ce dernier ? De même pour un verre de -8 dioptries.
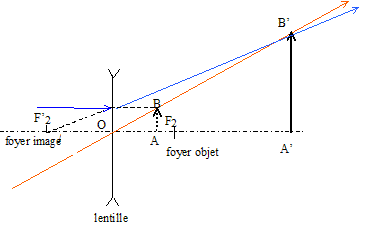
On note AB, l'objet et A'B' l'image de AB donnée par la lentille ; la lumière se déplace de la gauche vers la droite. Le schéma est "plus clair " si on le fait avec l'objet situé à 15 cm derrière la lentille
Par calcul : Les grandeurs écrites en bleu et en gras sont algébriques ( un signe + un nombre) vergence -5 d d'où OF'2 = -1/5 = -0 2 m objet situé 15 mm =0,015 m à gauche de la lentille donc OA =+0,015 m ; position de l'image OA'. Ecrire la relation de conjugaison : 1/OF'2 = 1/OA'- 1/OA 1/OA' = 1/OF'2 + 1/OA = -5 +1/0,015 = 61,67 soit OA' =1/61,67 = 0,0162 m = 16,2 mm grandissement transversal : g = OA' / OA = 16,2 / 15 = 1,08 ; image 1,08 fois plus grande que l'objet ( 20*1,08 = 21,6
mm ), de même sens que l'objet, située à gauche de la lentille, donc
réelle.
1/OA' = 1/OF'2 + 1/OA = -8 +1/0,015 = 58,67 soit OA' = 1/58,67 = 0,017 m = 17 mm grandissement transversal : g = OA' / OA = 17 / 15 = 1,136 ; image 1,136 fois plus grande que l'objet ( 20*1,136 = 22,7 mm ), de même sens que l'objet, située à gauche de la lentille, donc réelle.
|
|
|
|