Aurélie 20/3/6

forces pressantes sur une paroi

d'après concours interne d'ingénieur territorial 2003

En poursuivant votre navigation sur ce site, vous acceptez l’utilisation de Cookies vous proposant des publicités adaptées à vos centres d’intérêts.


. .

.
.


Hydraulique ( 3 pts)

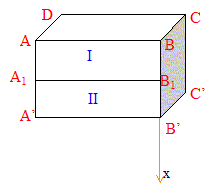
On considère un grand bassin rectangulaire rempli entièrement d'eau. AD=A'D'=BC=B'C'= l =4 m ; AB=A'B'=DC=D'C'=L=8 m ; AA'=BB'=CC'=DD'=H=9 m

La paroi verticale ABB'A' est formée de deux panneaux plans superposés ( I et II). On note AA1=h1 et A1A'=h2.

  1. Calculer les hauteurs h1 et h2 nécessaires pour que chaque panneau supporte la même force de pression due à l'eau.
  2. On fait un trou de section s= 5 cm² à la jonction de ces deux panneaux. Déterminer l'expression de la vitesse de sortie de l'eau puis la calculer.
  3. Calculer le débit volumique de l'eau au niveau de cet orifice. g= 9,81 m/s² ; masse volumique de l'eau r= 103 kg m-3.

corrigé
On note p0 la pression de l'air ambiant au dessus du liquide.

pression dans le liquide à une altitude x : la surface du liquide est l'altitude x=0 ; l'axe vertical est orienté vers le bas.

pression exercée par l'air + pression due à la hauteur de la colonne liquide : p = p0+ r g x

force élémentaire pressante due à l'eau sur une surface dS =Ldx de largeur L de hauteur dx située à l'altitude x :

dF= p dS = (p0+ r g x) Ldx dirigée vers l'extérieur du liquide

panneau (I), intégrer entre 0 et h1 : L[p0x+ ½r g x2] 0h1 =Lh1[p0+ ½r g h1 ].

force pressante exercée par l'air sur cc panneau (I) : p0Lh1, dirigée vers l'intérieur du liquide

soit au total : F1=½r g L h21, perpendiculaire au panneau et dirigé vers l'extérieur du liquide.

panneau (II), intégrer entre h1 et H : L[p0x+ ½r g x2] h1H =L[p0h2 +½r g ( H2-h21 )].

force pressante exercée par l'air sur ce panneau (II) : p0Lh2, dirigée vers l'intérieur du liquide

soit au total : F2=½r g L ( H2-h21 ), perpendiculaire au panneau et dirigé vers l'extérieur du liquide.

F1=F2 donne : h21=H2-h21 soit 2h21=H2 ou : h1 =2-½H.

h1 =0,707 H = 0,707*9 =6,4 m ; h2 = 9-6,4 = 2,6 m.

appliquer le théorème de Bernoulli entre l'eau à la sortie du trou ( notée T) et la surface libre (notée A)

La vitesse est quasiment nulle en A car la surface libre est très supérieure à la section du trou ; pA=p0=105 Pa ( pression atmosphérique)

A la sortie l'eau est en contact avec l'air pT= p0=105 Pa

½rvA²+pA+rg xA=½rvT²+pT+rg xB s'écrit : g xA=½vT²+g xB ; vT²= 2 g(xB - xA) = 2gh ( h : hauteur d'eau au dessus du trou)

vT= [2gh]½ ; si h= h1 alors vT= [2*9,8*6,4]½ = 11,2 m/s.

débit volumique correspondant ( m3/s ) = section (m²) fois vitesse (m/s) = 5 10-4*11,2 = 5,6 m3/s = 5,6 L/s.

retour -menu