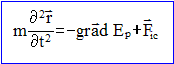|
Mouvement d'un solide ponctuel en microgravité ( mécanique ) En
poursuivant votre navigation sur ce site, vous acceptez l’utilisation
de Cookies vous proposant des publicités adaptées à vos centres
d’intérêts. |
||
| .
. |
||
|
||
|
|
référentiel géocentrique : solide formé par le centre de la terre et par les centres de 3 étoiles lointaines ; l'origine du repère est le centre de la Terre ; les trois axes pointent vers des étoiles lointaines qui paraissent fixes. Le référentiel géocentrique est pratiquement galiléen au voisinage de la Terre si on ne tient pas compte des attractions des autres astres. Placer un véhicule spatial ( masse m) ur une orbite circulaire autour de la Terre à l'altitude h = 300 km : L'étude est faîte dans le référentiel géocentrique 1ère méthode : ce véhicule est lancé verticalement depuis la surface de la Terre avec une vitesse v0 afin qu'il atteigne l'altitude h ; sa vitesse devient nulle ; on lui communique alors une vitesse horizontale v1. Calculs des vitesses en écrivant la conservation de l'énergie mécanique lors de la montée : énergie potentielle à la distance r du centre de la Terre : -mMG/r ( l'origine de cette énergie potentielle est prise à l'infini) à la surface de la Terre, l'énergie mécanique vaut : ½mv02 - mMG/R à l'altitude h où la vitesse est nulle, l'énergie mécanique vaut : - mMG/(R+h) L'énergie mécanique se conserve : ½mv02 - mMG/R = - mMG/(R+h) ; v02 =2MG[ 1/R - 1/(R+h]= 2MGh / (R(R+h)) De plus en assimilant le poids à l'attraction terrestre ( à la surface de la Terre) : mg = GMm/R² soit GM= g0R² d'où : v02 =2g0Rh / (R+h) = 2*9,8*6,37 106*3 105 / 6,67 106 =5,61 106 ; v0 =2370 m/s. Ecrire la 2è loi de Newton sur l'orbite circulaire : le satellite n'est soumis qu'à la force de gravitation de la Terre ; l'accélération est centripète de valeur aN= v12 / (R+h) ; d'où GMm/(R+h)2 = mv12 / (R+h) v12 =GM/(R+h) = g0R²/(R+h) ; v1 =R[g0/(R+h)]½= 6,37 106[9,8/6,67 106]½= 7721 m/s. vitesse angulaire du satellite : w= v1/(R+h) =1,16 10-3 rad/s. En réalité il est plus économique de : - Traverser verticalement l'atmosphère afin de limiter le freinage ; puis en modifiant l'inclinaison de la poussée du moteur on gagne l'orbite elliptique de Holmann dont l'apogée est l'altitude h. Cette apogée étant atteinte, on met à nouveau en marche le moteur pour obtenir la vitesse v1. - Dans le cas de satellite géostationnaire, dont l'orbite est dans le plan équatorial, il vaut mieux que la base de lancement soit proche de l'équareur.
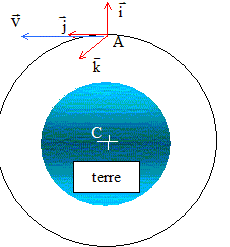
Le référentiel d'étude (r) est lié au satellite. Le centre de masse du satellite, noté A, est le centre de ce référentiel. L’objet est assimilé à un point matériel P de masse m repéré, dans (r), par les cordonnées du point P ( x, y, z) ; la position initiale P0 a les coordonnées (x0, y0, z0).
Forces s'exerçant, dans (r), sur l’objet P : attraction terrestre : force d'inertie : HP projection de CP sur la plan de la trajectoire du satellite ( les grandeurs écrites en bleu et gras sont des vecteurs) force de Coriolis : L’attraction terrestre dérive de l’énergie potentielle : -GMm/ CP= -m w2 (R+h)3/ CP. La force d'inertie centrifuge dérive de l’énergie potentielle : -½m w2 HP2. Energie potentielle totale de P : EP= -m w2 (R+h)3/ CP + -½m w2 HP2 = -m w2[(R+h)3/ CP+½HP2 ] Exprimons cette énergie potentielle au voisinage de A : x, y et z petits deavnt R+h. on note, pour simplifier l'écriture r= R+h ; avec : HP2 = (r+x)²+y²= r²+2rx+x²+y² et CP²=HP²+z² d'où 1/CP= ( r²+2rx+x²+y² +z²)-½ . mettre r² en facteur commun : 1/CP= r-1 ( 1+2x/r +(x²+y² +z²)/r²)-½ . Or : (1+e)-½ voisin de 1-½e +3/8 e ² avec e = 2x/r +(x²+y² +z²)/r² d'où : 1/CP= r-1[1-x/r -(x²+y² +z²)/ (2r²) + 3x²/(2r²)] soit EP= -mw2 r²[1-x/r -(x²+y² +z²)/ (2r²) + 3x²/(2r²)] -½mw2[ r²+2rx+x²+y²] = -mw2[1,5 r²-½(z²-3x²)]. force totale et équations différentielles régissant le mouvement de P : Ecrire la seconde loi de Newton : mx" = -dEp/dx+Fic x = 3mw2x + 2 mwy' (1) my" = -dEp/dy+Fic y = -2 mwx' (2) mz"= -dEp/dz+Fic z = -mw2z ou bien z" +w2z =0 (3) La solution de (3) est du type : z= z0 cos(wt+j) avec z(0)= z0 et z'(0) = 0 ; or z'= -z0 w sin (wt+j) d'où 0 = -z0 w sin j--> j=0 ou p. de plus z(0) = 0 = z0 cos j donne j=0. z= z0 cos(wt). Par intégration (2) devient : y'= -2w(x-x0) (4) Repport dans (1) : x"=3w2x - 4 w2(x-x0) soit x"+ w2x = 4 w2x0. la solution est du type : x= A cos(wt) + B sin(wt)+ 4x0. or x(0)=x0 soit x0 = A + 4x0 --> A= -3x0 ; de plus x'(0)=0 soit -Aw sin(0)+ Bw cos(0) =0 --> B=0 ; x= x0 (4-3cos(wt)). Repport dans (4) : y'= 6wx0[ cos(wt)-1] ; par intégration y = 6x0[ sin(wt)-wt] + y0. La trajectoire est une cycloïde décalée par rapport à l'axe des x. Initialement la force d'inertie centrifuge l'emporte ; puis la vitesse augmente et la force de Coriolis courbe la trajectoire. |
|
|
|
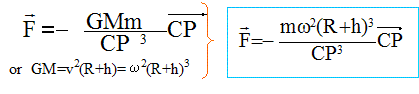
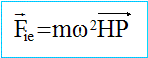
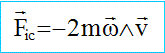 La force de Coriolis, perpendiculaire à la
vitesse, ne travaille pas.
La force de Coriolis, perpendiculaire à la
vitesse, ne travaille pas.