Résolution des équations différentielles en physique chimie

Aurélie 05/09/06

En poursuivant votre navigation sur ce site, vous acceptez l’utilisation de Cookies vous proposant des publicités adaptées à vos centres d’intérêts.

. .

Equation différentielle linéaire du second ordre : ax" + b x' + c x = f(t).

a, b, c sont des constantes ; x", x' respectivement dérivées seconde et première de la fonction x(t) par rapport au temps.

étape 1 : diviser tous les termes par a, afin que le coefficient de la dérivée seconde soit égal à 1.

ax" + b x' + c x = f(t) peut s'écrire : x" + 2l x' + w₀² x = f(t). (1)

La solution générale de l'équation différentielle (1) est la somme de la solution générale de l'équation différentielle sans second membre x" + 2l x' + w₀² x =0 et d'une solution particulière de (1).

étape 2 : recherche de la solution particulière

	solution particulière x_part
f(t) =A est une fonction constante	annuler x" et x' d'où x_part = Aw₀².
f(t) fonction sinusoïdale de pulsation w_exit. ( dans le cas d'oscillations forcées)	x_part(t) = A cos (w_exit t + B)
f(t) est une fonction exponentielle	x_part(t) : exponentielle du même type que f(t)

étape 3 : recherche de la solution générale de l'équation sans second membre x" + 2l x' + w₀² x =0

	type de solution
x" + w₀² x =0 ( oscillateur harmonique)	x(t) = A cos (w₀t+B) , A et B sont des constantes
x" - w₀² x =0	x(t) = A exp(w₀t) + b exp(- w₀t)
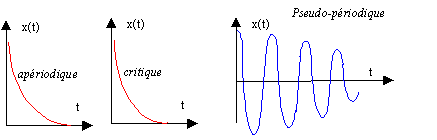
x" + 2l x' + w₀² x =0	Les solutions de cette équation différentielle dépendent du signe du discriminant de l'équation caractéristique associée : r²+2l r +w²₀=0 D = 4(l²-w²₀) D <0 frottement faible, régime pseudo-périodique en posant w = (w²₀-l²)^½; x(t) = exp(-lt) (A cos (wt+j) D =0, régime critique : x(t) = exp(- w₀t) ( At + B) D >0 ou l²>w²₀, régime apériodique en posant d=(l²-w²₀)^½ ; x(t) = exp(-lt)[A exp(dt) + b exp(- dt) ]

étape 4 : recherche des deux constantes d'intégration

utiliser les deux conditions initiales ( à t=0) en utilisant la solution générale de l'équation différentielle.

retour -menu