Aurélie 05/10/06

 

CAPES physique chimie ( d'après concours 2006 ) Le teslamètre.

En poursuivant votre navigation sur ce site, vous acceptez l’utilisation de Cookies vous proposant des publicités adaptées à vos centres d’intérêts.


. .

.
.


L'amplificateur opérationnel :

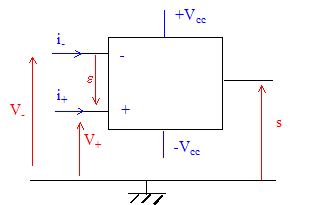
On schématise un amplificateur opérationnel (AO) par le schéma ci-dessous :

+Vcc et -Vcc : tension d'alimentation qui ne seront plus représentées par la suite ; V+ et V- sont les tensions d'entrée et s la tension de sortie ; e= V+ - V- est la tension différentielle d'entrée ; les intensités des courants d'entrée i+ = i- =0.

En régime linéaire l'AO est modélisé par :

 

  1. Qu'appelle t-on régime linéaire de fonctionnement ? Il existe un autre régime de fonctionnement de l'AO. Par quoi est-il caractérisé ?
  2. L'AO est inclus dans un montage suiveur alimenté par une tension sinusoïdale e(t) = E 2½ sin(wt). On associe à e(t) la tension complexe e = E 2½ e(jwt)

    Si on considère A infini, quelle conséquence cela implique t-il sur la valeur de e ? Cette condition étant remplie, en déduire la relation entre la tension complexe de sortie s et la tension d'entrée complexe e.

  3. On prend r=0 et A fini A=A0. Quel est en régime de fonctionnement linéaire, la relation liant s à e ? Sachant que A0 =105, la correction apportée est-elle significative ?
    - Quelle limite maximale ne doit pas dépasser E si on veut que le fonctionnement reste linéaire ?
    - Le montage précédent possède une boucle de rétroaction. Préciser ce que cela signifie ?
    - Avec l'hypothèse précédente, quelle est la valeur de la résistance de sortie du montage ?
  4. On prend maintenant r non nulle et A=A0. Le suiveur est alimenté par un générateur de tension continue E et de résistance interne Rg. Il est chargé par une résistance Ru comme indiqué ci-dessous :

    - Déterminer sa résistance d'entrée Re. La résistance de sortie Rs est définie comme le rapport de la tension de sortie à vide( Ru infinie) à l'intensité de sortie en court-circuit ( Ru=0). Montrer que Rs= r /(1+A0).
    - L'ordre de grandeur de r est de quelques dizaines d'ohms. Donner une expression approchée pour Rs et commenter le résultat. En déduire l'intérêt du montage suiveur.

Etude de quelques montages : ( AO idéaux en régime linéaire)
  1. Pour chacun des trois montages ci-dessous, établir les expressions donnant les tensions de sortie en fonction des grandeurs d'entrée et des valeurs des différentes résistances et en déduire la nature du montage.

    - Dans le montage 2, la résistance R3 peut varier entre 0 et R4. Entre quelles limites peut varier la tension de srtie s2 ?

Réalisation d'un teslamètre :

Le capteur est une sonde à effet Hall ; le constructeur donne la relation exprimant la tension de sortie UC en fonction de la valeur du champ magnétique B : UC= 0,5 Vcc + 13 B avec UC en volt et B en teslas. On désire par adjonction d'une chaîne électronique en sortie du capteur, obtenir une tension de sortie Us proportionnelle à B telle que Us= 102 B. Le synoptique de la chaîne est le suivant ( alimentations non représentées)/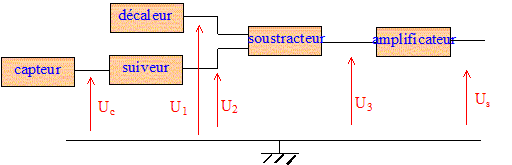

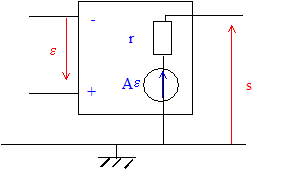
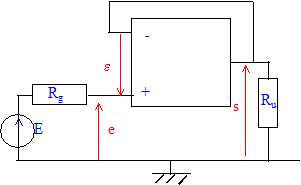
  1. Quel est l'intérêt du montage suiveur ?
  2. Quel est le rôle du décaleur ?
  3. On désire avoir U3=U2-U1 puis Us= 100 B. On réalise les différentes fonctions avec les montages précédents. Associer alors les blocs décaleur, soustracteur et amplificateur aux montages précédents. En déduire les valeurs des rapports R1/R2, R3/R4 et R5/R6 pour avoir la relation recherchée entre Us et B.
     
 


 corrigé
Régime linéaire de fonctionnement : la tension de sortie et la tension d'entrée sont proportionnelles.

L'autre régime de fonctionnement de l'AO : régime dit "saturé" : la tension de sortie vaut +Vcc si e est positive ou -Vcc si e est négative.

L'AO est inclus dans un montage suiveur alimenté par une tension sinusoïdale e(t) = E 2½ sin(wt). On associe à e(t) la tension complexe e = E 2½ e(jwt)

Si on considère A infini, la valeur de e est nulle.

Cette condition étant remplie, la relation entre la tension complexe de sortie s et la tension d'entrée complexe e est : s = e

On prend r=0 et A fini A=A0. En régime de fonctionnement linéaire, la relation liant s à e est :

V-= s =A0e ; V+ = e ; or e = V+-V- d'où : s =A0 (V+-V- )= A0 ( e-s) ;

s = A0 e / (A0 +1) = e/ (1+1/A0); si A0 = 105, alors s = e/(1+10-5) : la correction apportée n'est pas significative.
Limite maximale de E si on veut que le fonctionnement reste linéaire :

la tension de sortie doit être inférieure à Vcc soit E<Vcc2-½.
Boucle de rétroaction : on injecte une partie ou toute la tension de sortie vers l'entrée de l'AO.
La valeur de la résistance de sortie du montage vaur r =0.

r non nulle et A=A0. Le suiveur est alimenté par un générateur de tension continue E et de résistance interne Rg. Il est chargé par une résistance Ru.

L'intensité des courants d'entrée étant nulle, alors la résistance d'entrée Re est infinie.

La résistance de sortie Rs

intensité de sortie en court-circuit ( Ru=0) : icc = A0e/r avec e = V+-V- = E-0 ; icc = A0E/r

tension de sortie à vide( Ru infinie) : s = A0e = A0 (E-s) soit s = A0 E / (A0 +1)

Or Rs= s / icc d'où : Rs= r /(1+A0).

L'ordre de grandeur de r est de quelques dizaines d'ohms et A0 = 105 d'où : Rs voisin de 10-5 r voisin 10-4 W, quasiment nulle.

Le montage suiveur permet de réaliser un générateur de tension parfait.

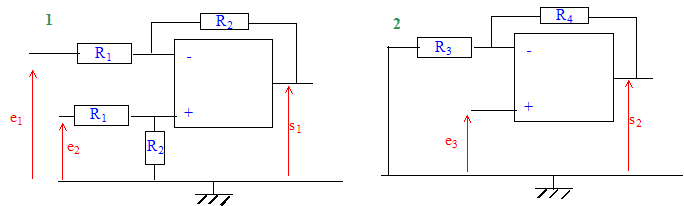
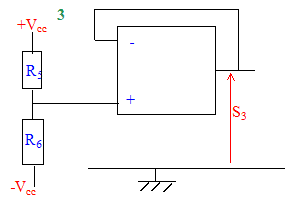
montage 1 : amplificateur soustracteur

Théorème de Millmann appliquée à l'entrée non inverseuse : V+ = [e2/R1 ] / [1/R1 + 1/R2]

Théorème de Millmann appliquée à l'entrée inverseuse : V- = [e1/R1 + s1/R2] / [1/R1 + 1/R2]

V+ =V- donne : e2/R1 = e1/R1 + s1/R2 soit s1 = R2/ R1 ( e2-e1)

montage 2 : amplificateur non inverseur

Théorème de Millmann appliquée à l'entrée inverseuse : V- = [ s2/R4] / [1/R3 + 1/R4]

de plus V+=V-=e3 d'où e3= [ s2/R4] / [1/R3 + 1/R4]

e3 [1/R3 + 1/R4]= s2/R4 ; s2= e3(R3 +R4) / R3.

La résistance R3 peut varier entre 0 et R4 ; donc s2 peut varier entre +Vcc et 2e3.

montage 3 : générateur de tension continue réglable

Théorème de Millmann appliquée à l'entrée non inverseuse : V+ = [Vcc/R5 - Vc c/R6] / [1/R5 + 1/R6]

de plus V+=V-=s3 d'où s3= Vcc ( R6-R5]) / (R6+R5).

Intérêt du montage suiveur : adapter l'impédance, en sortie on aura toujours RS=0.

Rôle du décaleur : d'après le constructeur UC= 0,5 Vcc + 13 B

il faut éliminer 0,5 Vcc pour que la tension de sortie soit proportionnelle au champ magnétique.

Associer alors les blocs décaleur, soustracteur et amplificateur aux montages précédents :

montage n°3 : décaleur ; montage n°1 : soustracteur ; montage n°2 : amplificateur.

On désire avoir U3=U2-U1 puis Us= 100 B.

U2 = Uc (montage suiveur) ;

U3 = R2/ R1 ( U2 -U1) (donné par le montage soustacteur) ; de plus il faut U3 = U2 -U1 d'où R2/ R1 = 1.

U3 = U2 -U1 = Uc-U1 = 0,5 Vcc + 13 B-U1

U3 doit être proportionnelle à B donc : 0,5 Vcc=U1 et U3 = 13 B.

D'autre part d'après le montage n°2 : Us = U3(R3 +R4) / R3

soit 100 B = 13 B(R3 +R4) / R3 ; 100 R3 = 13 R3 + 13 R4 soit : R3/R4 = 13/87 =0,15.

d'après le montage n°3 : s3= Vcc ( R6-R5) / (R6+R5) et 0,5 Vcc=U1

0,5 = ( R6-R5]) / (R6+R5) ; R6+R5 =2R6-2R5 ; R6 = 3 R5 ; R5/R6 = 1/3.



retour -menu