Aurélie 09/06

 

CAPES physique chimie ( concours interne 2006 ) électrocinétique : RLC série

En poursuivant votre navigation sur ce site, vous acceptez l’utilisation de Cookies vous proposant des publicités adaptées à vos centres d’intérêts.


. .

.
.


Electrocinétique :

Le circuit comporte un générateur de tension sinusoïdale uNM = U1 cos (wt) de fréquence f, un conducteur ohmique R= 10 W, une bobine d'inductance L et de résistance négligeable et un condensateur de capacité C= 2,0 10-5 F. La valeur efficace de la tension délivrée par le générateur vaut U1 = 10 V.

La tension uNM est visualisée à l'oscilloscope voie 1 et la tension uBM voie 2. La base de temps vaut 2,5 10-3 s par carreau. 5,0 V / div. A la date t=0, la tension uNM(t) est maximale sur l'oscillogramme.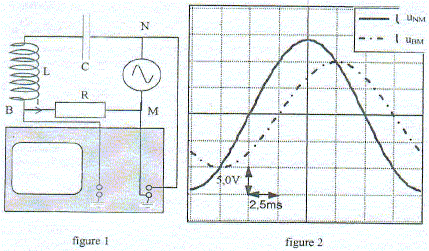

  1. Déterminer la fréquence f.
  2. Déterminer la phase j de la tension uNM par rapport à l'intensité i du courant.
  3. Donner les expressions des tensions instantanées uNM(t) et uBM(t) en fonction du temps, de la fréquence f et de la phase j et des tensions maximales respectivement U1max et U2max dont on donnera les valeurs numériques.
  4. Définir "intensité efficace". Comment la mesurer directement ? Déterminer 'intensité efficace I du courant.
  5. Rappeler l'expression de l'impédance complexe des dipôles suivants : conducteur ohmique de résistance R, bobine pure d'inductance L, condensateur de capacité C pour une fréquence f.
    - Donner l'expression de l'impédance complexe équivalente aux dipôles compris entre les points N et M.
    - Déterminer la valeur numérique du module de l'impédance du circuit Z.
  6. En déduire l'expression de L puis sa valeur numérique.
corrigé
La fréquence f :

Une période correspon à 8 carreaux sur le graphe soit T= 8*2,5 10-3 = 0,02 s ; la fréquence est l'inverse de la période, exprimée en seconde : f= 1/0,02 = 50 Hz.

La phase j de la tension uNM par rapport à l'intensité i du courant :

La tension uBM aux bornes du conducteur ohmique est l'image de l'intensité au facteur R près.

La tension uNM est en avance de un carreau sur l'intensité ( lecture graphe) soit le huitième de la période soit j =2p/8 = p /4 rad

Expressions des tensions instantanées uNM(t) et uBM(t) en fonction du temps, de la fréquence f et de la phase j et des tensions maximales respectivement U1max et U2max dont on donnera les valeurs numériques :

uNM(t) = U1max cos ( 2pft) ; U1max : lecture graphe 2,8 carreaux soit 2,8*5 = 14 V

uBM(t) = U2max cos ( 2pft- p /4) ; U2max : lecture graphe 2 carreaux soit 2*5 = 10 V

Définir "intensité efficace":

valeur du courant continu qui passant dans le même conducteur ohmique pendant le même temps produirait le même effet Joule.

On mesure l'intensité efficace en plaçant un ampèremètre en série dans le circuit : Imax =U2max /R = 1 A ; I= 1/1,414 = 0,7 A.

Expression de l'impédance complexe des dipôles :

conducteur ohmique de résistance R : R

bobine pure d'inductance L : jLw= jL2pf

condensateur de capacité C : -j/(Cw)
Expression de l'impédance complexe équivalente aux dipôles compris entre les points N et M :

Z = R + j(Lw-1/ (Cw))
Valeur numérique du module de l'impédance du circuit Z : Z= U1max / Imax = 14/1 = 14 ohms.

Expression de L puis sa valeur numérique :

Z= [R² + (Lw-1/ (Cw)²]½= 14

R² + (Lw-1/ (Cw)² = 14² = 196 ; (Lw-1/ (Cw)² = Z²-R²

Lw-1/ (Cw ) = [Z²-R²]½ ; Lw = [Z²-R²]½ +1/ (Cw ) ; L= { [Z²-R²]½ +1/ (Cw )}/w

w = 2pf = 314 rad/s ; L={ (196-100)½ +1/(2 10-5*314)}/314 =0,54 H.



Réponse d'un circuit RLC à un échelon de tension :

On remplace dans le circuit précédent le générateur fonctionnant en alternatif par un générateur de tension continue de fem E= 5 V en série avec un interrupteur K. Le condensateur est primitivement déchargé et l'interrupteur est ouvert. A la date t=0 on ferme l'interruteur K.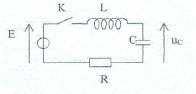

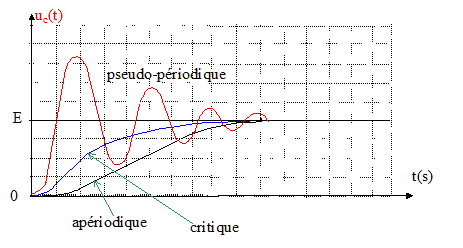
  1. Donner l'équation différentielle exprimant la tension uc(t) aux bornes du condensateur en fonction des paramètres du circuit.
  2. Résoudre cette équation et donner l'expression littérale de uc(t).
  3. Quelle valeur littérale aurait-il fallu donner à R pour obtenir le régime critique ? Dans ce cas donner l'allure de la courbe uc(t).
    - Quelle application pratique présente ce régime ?
    - Avec la valeur R= 10 ohms, quel est le régime de fonctionnement du circuit ?
  4. Proposer un montage permettant de visualiser les régimes transitoires en précisant les connexions à l'oscilloscope. Quelle type de tension doit délivrer le générateur ? Quelle condition doit-on imposer à la période de la tension délivrée par le générateur ?
    - Actuellement de quel autre moyen dispose t-on pour visualiser ces régimes ?
corrigé
Equation différentielle exprimant la tension uc(t) aux bornes du condensateur en fonction des paramètres du circuit :

additivité des tensions aux bornes des dipôles : uc + Ri + Ldi/dt = E

de plus i = dq/dt et q=Cuc d'où i= Cduc/dt et di/dt = Cd²uc/dt²

d'où : uc +RCduc/dt + LCd²uc/dt² = E

ou encore : LC u"c + RC u'c + uc = E.

Résolution et expression littérale de uc(t) :

La solution générale de l'équation différentielle est la somme :

- d'une solution particulière ( régime permanent) uc = E.

- de la solution générale de LC u"c + RC u'c + uc = 0

diviser tous les termes par LC, afin que le coefficient de la dérivée seconde soit égal à 1.

u"c + R/L u'c + 1/(LC) uc = 0

On pose l = R/(2L) ; de plus 1/(LC) = w0² ( pulsation propre du dipôle LC)

u"c +2l u'c + w0² uc = 0

équation caractéristique associée : r² + 2l r +w0² = 0 ; discriminant réduit : D '=l²- w0² .

Trois cas sont possibles :

Si l <w0 régime pseudo-périodique : uc = A exp(-l t) cos(w0t+j) + E

Si l >w0 : régime apériodique (surcritique) : r1= -l +D'½ ; r2= -l -D'½ ;

uc = A exp(r1t)+B exp(r2t) + E

Si l =w0 : régime critique : uc = exp(-lt)*(At+B) + E

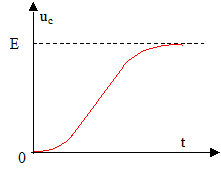
En mécanique ( véhicules) , le régime critique assure un meilleur confort aux passagers en évitant les oscillations ; le retour du système à l'équilibre est le plus rapide. Il en est de même en électricité, on évite des oscillations.

De plus la courbe rouge ci-dessus ( régime pseudo-périodique) met en évidence une surtension aux bornes du condensateur , surtension qui est évitée ( courbe bleue)

Valeur littérale de R pour obtenir le régime critique : D = R²C²-4 LC =0 soit R= [4L/C]½ = [4*0,54/2 10-5]½ = 329 ohms

Avec la valeur R= 10 ohms, le régime de fonctionnement du circuit est une charge pseudo-périodique du condensateur.

Allure de la courbe uc(t) dans le cas du régime critique :

Montage permettant de visualiser les régimes transitoires :

utiliser un GBF à masse flottante, délivrant un signal rectangulaire dont la période est plus grande que la durée de la charge du condensateur.

Visualiser la tension aux bornes du condensateur.

On peut remplacer l'oscilloscope par un oscilloscope à mémoire ou bien utiliser un ordinateur + interface + logiciel de traitements des données.

retour -menu