|
Deux boules dans l'espace ( d'après
concours Mines 74) En
poursuivant votre navigation sur ce site, vous acceptez l’utilisation
de Cookies vous proposant des publicités adaptées à vos centres
d’intérêts.
|
||
| .
. |
||
|
||
|
|
Deux boules homogènes ont même rayon a/4, même masse, même masse volumique r = 7800 kg m-3. Le référentiel est galiléen. Le centre de l'une est fixe en O, origine d'un axe Ox ; le centre de l'autre est en un point M d'abscisse x>0. La seule force appliquée à la boule de centre M est la force gravitationnelle exercée par l'autre boule. On peut remplacer chaque boule par un point matériel, de centre O ou M, et de même masse.
La boule M est soumise à la force gravitaitonnelle attractive, exercée par la boule O.
vitesse lorsque son centre se trouve à l'abscisse x : méthode 1 : écrire le théorème de l'énergie cinétique entre l'instant initial d'abscisse x= a, de vitesse nulle et l'instant final d'abscisse x, de vitesse v. La force F et le déplacement sont des vecteurs colinéaires et de même sens : le travail de cette force est moteur.
méthode 2 : utiliser la conservation de l'énergie mécanique. L'énergie potentielle de pesanteur à la distance x s'exprime par : Ep = -Gm2/x. L'origine de cette énergie est prise à l'infini. -Gm2/x + ½mv2 = -Gm2/a par suite v² = 2Gm[1/x - 1/a] La boule M est attirée par la boule O : le vecteur vitesse est orienté vers O, en sens contraire de l'axe et sa valeur est : v = [ 2Gm(1/x - 1/a)]½.
instant t pour lequel M se trouve à l'abscisse x : la vitesse est la dérivée de l'abscisse par rapport au temps : v = dx/dt ; dt = dx/v puis intégrer entre a et x.
instant t1 du choc en fonction de G et r : D'une part les deux boules de rayon r = 0,25 a, se heurtent lorsque x = ½a. d'autre part f(½a ) = - a3/2 [p/4+½] enfin la masse de la boule M s'exprime par : volume * masse volumique m = Vr avec V= 4/3p(a/4)3 d'où m = pra3 / 48 t1 = -f(½a) [2Gm]-½ = a3/2 [p/4+½] [1/24 Gpra3]-½ = [p/4+½] [1/24 Gpr]-½ t1 = (3,14/4 + 0,5)[ 6,67 10-11 * 3,14 *7800 /24]-½ = 4925 s. équation différentielle du second ordre à laquelle obéit la distance x entre les centres des deux boules : Le centre de masse des deux boules de même masse est située au milieu du segment OM. Ce centre de masse est fixe et les deux boules se déplacent symétriquement par rapport au centre de masse ; x étant la distance séparant les deux boules, l'abscisse de M est ½x, tandis que l'abscisse de O est -½x. La seconde loi de Newton s'écrit alors : md²(½x) / dt² = -Gm²/x² soit md²x/dt² =-2Gm²/x² dans l'étude précédente cette même loi s'écrivait : md²x/dt² = -Gm²/x² Pour la calcul de t2 il suffit de remplacer dans l'expression de t1, G par 2 G : d'où t2 = 2-½t1 = 3483 s. Le choc entre les deux boules est élastique : Les boules rebondissent l'une sur l'autre ; après le choc les boules s'éloignent symétriquement : leurs vecteurs vitesses on même valeur mais sont de sens contraire. Lorsque la distance de leurs centres est égale à x=a, elles s'immobilisent puis enssuite elles vont se rapprocher. Le mouvement est périodique, de période 2t2. Le choc entre les deux boules est mou : A chaque choc la moitié de l'énergie cinétique est dissipée en chaleur ; après chaque choc les valeurs des vitesses sont divisées par 2½. Les rebonds seront donc de plus en plus petits ; les deux boules s'immobiliseront l'une contre l'autre. |
|
|
|
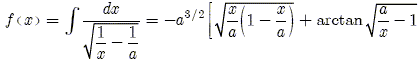
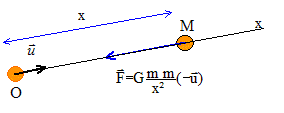
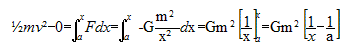
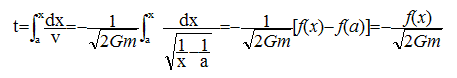 ; f(a)
étant nulle.
; f(a)
étant nulle.