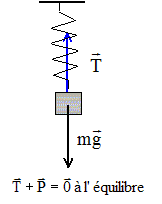|
En
poursuivant votre navigation sur ce site, vous acceptez l’utilisation
de Cookies vous proposant des publicités adaptées à vos centres
d’intérêts. |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| .
. |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
Un faisceau de lumiere monochromatique traverse un hémi-cylindre en verre ; il passe par le centre O de celui-ci.
corrigé 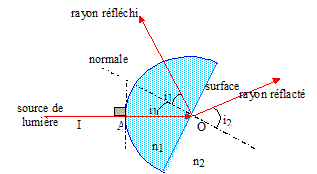
Loi de Descartes pour la réfraction : n1 sin i1 = n2 sin i2. sin i1 = n2 / n1 sin i2 = 1/1,5 sin 40 = 0,428 i1 = sin -1 (0,428) = 25°.
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Un paquebot de masse de 8000 tonnes est immobile dans un port.
corrigé 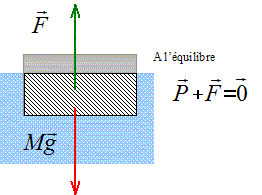
Le navire est soumis : à son poids, verticale, vers le bas, valeur P=mg m : masse du navire = 8 106 kg à la poussée d'Archimède, verticale , vers le haut, valeur : F= g r V r : masse volumique eau de mer (1030 Kg.m-3) V : volume de la partie immergée (m3) ; g = 10 N/kg. D'après le principe d'inertie, ces deux forces sont opposées : elles ont la même valeur. mg = g r V soit m = r V d'où : V= m/r = 8 106 / 1030 = 7,8 103 m3.
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
On souhaite construire un dynamomètre en utilisant un ressort à spires non jointives. Pour étalonner ce dynamomètre, une extrémité du ressort est fixé à un support, à l'autre extrémité on accroche des masses marquées. L'allongement du ressort est déterminé par l'ombre du dispositif sur un écran ( feuille de papier millimétré. Le ressort est placé à égale distance ( D= 1 m) de la lampe et de l'ecran. On repère alors l'ombre de l'éxtrémité du ressort sur la feuille.
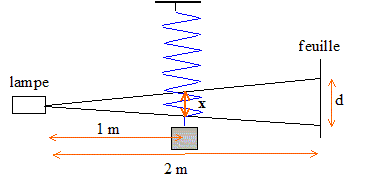
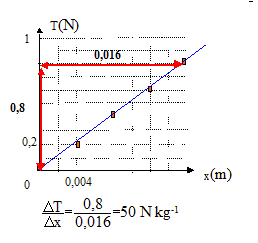
L'extrémité inférieur du ressort est soumise à : l'action de la masse, verticale vers le bas, valeur P=mg ( masse en kg) à la tension du ressort, verticale vers le haut, valeur T= k x ( k : raideur en N/kg et x : allogement en m) T= mg = kx
la raideur k est égale au coeficient directeur de la droite.
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|