Les voies ferrées sont "relevées" dans les virages, ( inclinées d'un angle "alpha" faible par rapport à l'horizontale).
Le train décrit un virage à vitesse constante. Le centre d'inertie G d'un wagon de masse M= 30 tonnes a une trajectoire circulaire de rayon R, de centre O.

1. Quels sont la direction et le sens du vecteur variation de vitesse de G lorsque le train prend le virage ?

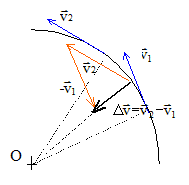
le vecteur variation de vitesse est , dirigé vers le centre O, porté par le rayon du cercle au point considéré.

2. On note vecteur F la somme des forces autres que le poids P exercées sur le wagon. F est perpendiculaire au plan des rails. Quelles sont les caractéristiques de la somme vectorielle des forces exercées sur le wagon dans un référentiel terrestre ?

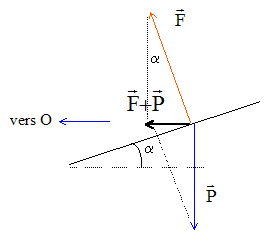
La somme vectorielle des forces est et de même sens que le vecteur variation du vecteur vitesse ( 2ème loi de Newton)

3. Calculer "alpha" pour F= 2,95,0 10 ^ 5 N ; g= 10 N/kg.
cos "alpha" =P/F
Poids(N) = masse (kg) *10 = 30 10^3 *10 = 3,0 10^ 5 N
cos "alpha" = 2,95/3 = 0,983 soit "alpha" = °
( valeur plus précise 10,5° pour la suite des calculs)

4. Exprimer puis calculer h, différence de hauteur ou "dévers" entre le rail extérieur et le rail intérieur ; la distance entre les deux rails est d=1,44 m.
h = d sin "alpha" = 1,44 sin 10,5 = m.