Un insecte de masse m = 1,0 g se déplace sur le bord d'un disque ( masse M=0,50 kg ; rayon R= 15 cm ). Quel est le déplacement du disque lorsque l'insecte effectue un tour complet ( retour au point de départ) ? Les frottements sont négligés.

L'insecte en se déplaçant entraîne le disque ;ce dernier tourne plus lentement que l'insecte.
Ecrire la conservation du moment cinétique du système {insecte, disque}

Moment d'inertie du disque : I1=½MR²
M = 0,5 kg, R = 0,15m : I1 = 0,5*0,5*0,15²= 5,62 10^-3 m²
Moment d' inertie de l'insecte : I2 = mr²
m = 10^-3 kg et r = 0,15 m : I2 = 10^-3*0,15² =2,25 10^-5 kg m²
Conservation du moment cinétique :
I1 . "omega"1 = I2 . "omega"2
où "omega"1 et "omega"2 sont respectivement les vitesses angulaires (/s) du disque et de l'insecte.


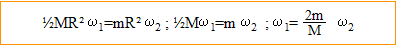
De plus les vitesses angulaires sont constantes, donc proportionnelles aux balayés.

L'insecte fait un tour ; l'angle balayé est "alpha"2 = 2 pi radians.
Le disque tourne de l'angle "alpha"1 pendant le même temps.

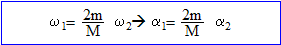
"alpha"1 = 2 10^-3 / 0,5 * 6,28 = 10^ -2 rad.
ou bien "alpha"1*180 / 3,14 = 1,4 degrés.