Une rame de métro comprend trois wagons. Masse d'un wagon M= 1,2 10^5 N. Force de frottement exercée sur chaque wagon f= 1,0 10^3 N. Le premier wagon, exerce une force motrice F= 6,0 10^4 N.

1. Quelle est l'accélération de la rame ?
Système étudié : les trois wagons ; référentiel terrestre galiléen.

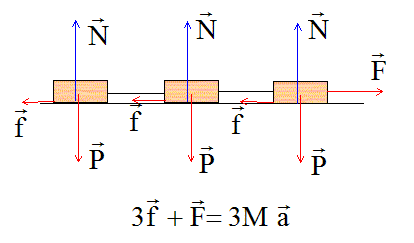
La seconde loi de s'écrit sur un axe horizontal, dirigé vers la droite : F-3f= 3Ma
a=( F/3-f) / M= (2 10^4 - 10^3)/1,2 10^5 = m/s²
( on conserve une valeur plus précise pour la suite des calculs : 0,1583 )

2. Quelle est la valeur de la force de traction exercée entre le premier et le second wagon ?
Système étudié : le premier wagon seul.

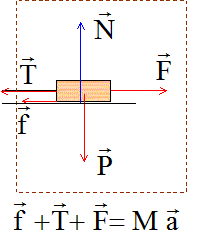
Ecrire la seconde loi de Newton sur un axe horizontal orienté vers la droite :
-f-T+F= Ma
T= F-Ma-f = 6 10^4 -1,2 10^5 *0,1583- 10^3 = 10^4 N

3. Quelle est la valeur de la force de traction exercée entre le second et le troisième wagon ?

Système étudié : le second wagon seul.

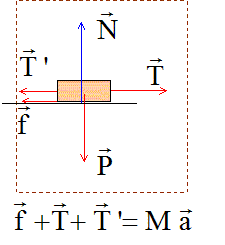
Ecrire la seconde loi de Newton sur un axe horizontal orienté vers la droite :
-f+T-T '= Ma
T '= T-Ma-f = 4 10^4 -1,2 10^5 *0,1583- 10^3 = 10^4 N