Aurélie 21/12/05
Ondes, diffraction, réfraction : goutte d'eau, ondes transversales

d'après concours ESIEE 05 ( répondre par vrai ou faux )

exercice suivant : radioactivité

Balise à la surface de l'eau

Une balise, immobile à la surface de l'eau, émet un signal détecté par un dirigeable et un sous marin, tous les deux supposés immobiles à la verticale de la balise. Le dirigeable détecte le signal 2 s après son émission. Le sous marin se situe à 128 m de profondeur. La vitesse du son dans l'air vaut vair = 320 m/s.

On note veau la vitesse du son dans l'eau. L'une des deux vitesses est cinq fois plus grande que l'autre.

  1. vair est-elle plus grande que veau ?
  2. Le sous marin détecte-t-il le signal 2 s après son émission ?
  3. Le dirigeable est-il à 640 m d'altitude ?
  4. La balise émet un signal toutes les trois secondes :
    - La fréquence des signaux enregistrés par le sous marin est-elle inférieure à celle des signaux enregistrés par le dirigeable ?
    - Le sous marin et le dirigeable détectent-ils un signal toutes les trois secondes ?
corrigé
vair est plus petite que veau

veau = 5 vair = 5*320= 1600 m/s.

Le sous marin détecte un signal à la date : distance (m) / vitesse (m/s)= 128/1600 = 0,08 s.

Altitude du dirigeable : vitesse (m/s) * temps (s) = 320*2 = 640 m

La fréquence des signaux enregistrés par le sous marin est égale à celle des signaux enregistrés par le dirigeable, balise, dirigeable et sous marin sont immobiles.

Le sous marin et le dirigeable détectent un signal toutes les trois secondes
Diffraction

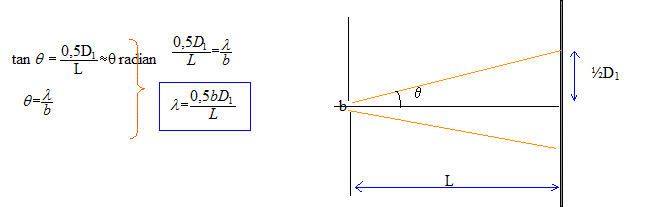
On observe sur un écran la figure de difraction ci-dessous d'un faisceau laser de longueur d'onde l à travers une fente fine de longueur a et de largeur b située à la distance L de l'écran. On note q l'écart angulaire, angle sous lequel est vue la moitié de la tache centrale depuis l'objet diffractant.

L= 2 m ; D1 = 1 cm ; D2 = 1 mm ; a = 1 cm ; b = 0,2 mm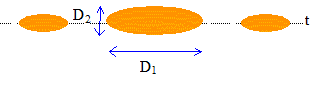

  1. La direction "t" est-elle dans le sens de la longueur de la fente ?
  2. q vaut-il 0,25 10-2 radian ou bien 0,25 10-3 radian ?
  3. La longueur d'onde vaut-elle l =500 nm ou bien l =410 nm ?
corrigé
La direction "t" est perpendiculaire à la longueur de la fente verticale.

q = 0,5 D1/L =0,5 *10-2 / 2 =0,25 10-2 radian

l = 0,5 * 2 10-4* 10-2 / 2 =0,5 10-6 m = 500 nm.

réfraction : goutte d'eau

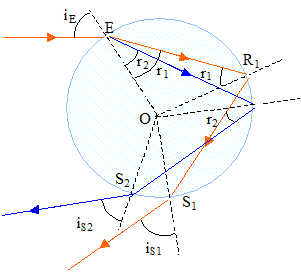
La goutte d'eau est supposée sphérique. Sur le schéma figurent la trajectoire de la lumière de longueur d'onde l1 ( réfraction suivant ER1, puis réflexion suivant R1S1, réfraction en S1 et sortie sous l'angle iS1) et le rayon émergeant en S2 avec un agle iS2 correspondant à une longueur d'onde l2. L'indice de l'eau est une fonction décroissante de la longueur d'onde. nair = 1.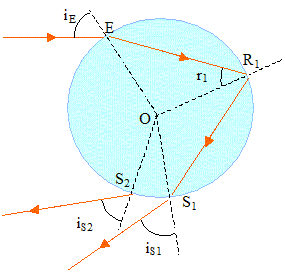

  1. l1 est-elle inférieure à l2 ?
  2. iS1 est-il égal à iSE ?
  3. iS1 est-il égal à iS2 ?
  4. On donne la célérité c de la lumière dans le vide et les fréquences nviolet et nrouge des radiations violette et rouge dans l'air : c = 3 108 m/s ;
    nviolet =7,5 108 MHz ; nrouge =3,75 108 MHz .
    - lviolet vaut-elle 400 nm ?
    - Dans un arc en ciel simple, l'arc rouge est-il au dessus du violet ?
corrigé
réfraction en E :

pour la radiation de longueur d'onde l1 : nair sin iE = n1 sin r1 ;

pour la radiation de longueur d'onde l2 : nair sin iE = n2 sin r2 ;

n1 sin r1 = n2 sin r2 ;

Dans l'hypothèse "l1 est inférieure à l2 " : n1 < n2 et donc sin r1 >sin r2 ; r1 > r2 .

 

réfraction en S1 : n1 sin r1 = nair sin iS1.

Or nair sin iE = n1 sin r1 d'où : iS1 = iE.

réfraction en S2 : n2 sin r2 = nair sin iS2.

Or nair sin iE = n2 sin r2 d'où : iS2 = iE = iS1.

lviolet = c/ nviolet =3 108 / 7,5 1014 =4 10-7 m = 400 nm
Dans un arc en ciel simple, l'arc rouge est dessus du violet.
Onde transversale

Une onde transversale de longueur d'onde l se propage avec une vitesse v inférieure à 10 m/s, de la gauche vers la droite, le long d'une corde supposée infinie. On note P1 et P2 deux points de la corde distants de L= 10 cm, P1 à gauche de P2.

Les figures ci-dessous représentent l'allure de la déformation y(t) de la corde en fonction du temps aux points P1 et P2 :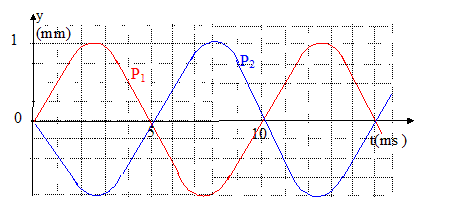

  1. P1 et P2 vibrent-ils en phase ?
  2. L est-elle égale à (2n+1) l avec n entier ?
  3. L est-elle égale à (2n+1) l/2 avec n entier ?
  4. On prend la plus petite valeur possible de n :
    - l vaut-elle 20 cm ?
    - v vaut-elle 6,6 m/s ?
corrigé
P1 et P2 vibrent en opposition de phase.

P1 et P2 sont distants d'un nombre impair de demi longueur d'onde : L= 0,1= (2n+1) l/2.

La plus petite valeur possible pour n est n= 0 : d'où l = 20 cm.

période : T= 10 ms = 0,01 s (lecture graphe)

célérité (m/s) = longueur d'onde (m) / période (s) = 0,2 / 0,01 = 20 m/s.
retour -menu