I
Une masse m=25 g est attachée à l'extrémité d'un ressort horizontal, de constante de raideur k= 0,2 N/m et de longueur à vide Lo= 10 cm. L'autre extrémité du ressort est fixée à un point fixe O.
A est le point d'abscisse OA = 12 cm et B est le point d'abscisse OB= 8 cm.
On lâche m de A avec une vitesse nulle. Cette masse se déplace sans frottement sur le plan horizontal selon l'axe Ox.

1. L'énergie potentielle élastique de m en A vaut-elle 0,04 mJ ?

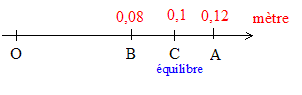
En A la déformation du ressort vaut : |longueur - longueur initiale| = x= m
Energie potentielle élastique en A : Ep(A) = ½kx² = 0,5*0,2 (0,02)² = 4 10^ - 5 J = 0,04 mJ.

2. L'énergie potentielle élastique de m en B vaut-elle 0,64 mJ ?
En B la déformation du ressort vaut : longueur - longueur initiale = x=0,02 m
La déformation en B est identique à la déformation en A : donc l'énergie potentielle élastique en B est à l'énergie potentielle élastique en A.

3. La pulsation du mouvement vaut-elle 8 rad/s ?
pulsation au carrée = raideur (N/m) masse (kg) = 0,2 / 0,025 = 8
La pulsation vaut : racine carrée (8)

4. L'énergie cinétique de m lorsque m est au milieu de [AB] vaut-elle 0,04 mJ ?
En C, milieu de [AB], le ressort n'est pas déformé : l'énergie mécanique du système {masse + ressort} est sous forme : ½mv²
En B, m est immobile : l'énergie mécanique du système {masse + ressort} est sous forme : ½kx² ( avec x= 0,02 m)
L'énergie mécanique se ( frottements négligés)
Energie cinétique en C = énergie potentielle élastique en A= 0,04 mJ.

5. L'énergie mécanique de m en A vaut-elle 1,44 mJ ?
Energie cinétique en C = énergie potentielle élastique en A= énergie mécanique= 0,04 mJ


II
A l'instant t=0, on lâche sans vitesse initiale, une bille pleine sphérique de masse volumique "ro", dans un fluide de masse volumique "ro' ". Outre son poids et la poussée d'Archimède, la bille est soumise à une force de frottement fluide, colinéaire à la vitesse et de sens contraire, de valeur kv ( k est une constante). La taille du récipient est supposée très grande.

1. La vitesse tend-elle vers une valeur limite proportionnelle à k ?

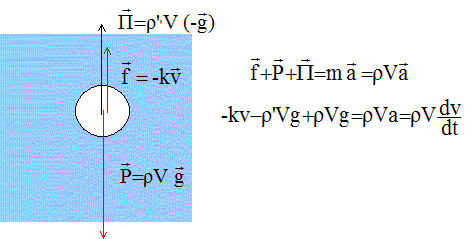
Quand la vitesse limite est atteinte, les forces se .
-kv(lim) - ro' Vg + ro Vg=0
v(lim) = Vg(ro-ro')/ k.


2. L'accélération initiale de la bille est-elle nulle ?
A t=0, la vitesse est nulle : la force de frottement fluide est donc .

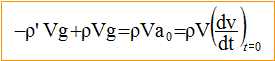
si "ro" est différent de "ro' " l'accélération initiale n'est pas nulle.

3. Au bout d'un certain temps le mouvement devient-il uniformément accéléré ?
Au bout d'un certain temps, les forces se neutralisent ; d'après le principe d'inertie, la bille est animée d'un mouvement rectiligne .

4. A t=0, l'accélération vaut-elle : (ro - ro') g / ro ?


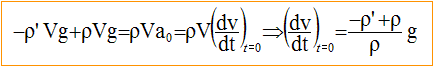
5. L'accélération de la bille à t=0 dépend-elle de k ?
L'accélération initiale ne dépend pas de k.