I. Un mobile est animé d'un mouvement rectiligne. Sa vitesse est représentée figure 1.

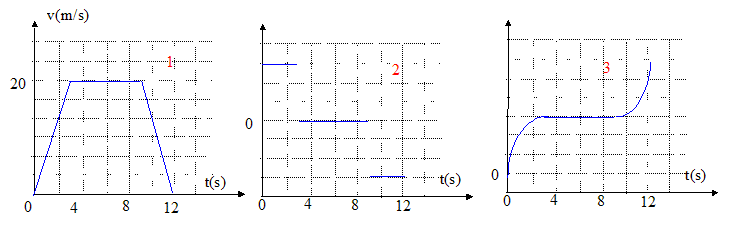
1. La figure 2 représente-t-elle l'accélération ?
Le vecteur accélération est la par rapport au temps du vecteur vitesse.
entre 0 et 3 s : la vitesse est une fonction linéaire , son coefficient directeur, donc la valeur de l'accélération, est positif.
entre 3 et 9 s : la vitesse est constante ; donc l'accélération est nulle.
entre 9 et 12 s : la vitesse est une fonction affine , son coefficient directeur, donc la valeur de l'accélération est négative.
Donc le graphe 2 représente l'accélération.

2. La figure 3 représente -t-elle la distance parcourue ?
La distance est une de la vitesse.
entre 0 et 3 s : v= 20/3 t ; distance parcourue D1 = ½ 20/3 t² = 10/3 t² ( branche de , concavité vers le haut )
entre 3 et 9 s : v= 20 m/s : distance parcourue D2 = 20 t ( fonction linéaire croissante et non pas constante comme sur le graphe 3)
entre 9 et 12 s : v= -20/3 t ; distance parcourue D3 = 10/3 t² ( branche de parabole, concavité vers le bas).
Donc le graphe 3 de convient pas.

3. Les vecteurs accélération et vitesse sont-ils toujours orientés dans le même sens ?
Vecteurs accélération et vitesse sont colinéaires :
de même sens entre 0 et 3 s : la vitesse augmente
de sens entre 9 et 12 s : la vitesse diminue.

4. Le mobile fait-il demi-tour à t= 9 s ?
A partir de t= 9 s, la vitesse diminue et le mobile s'arrète à t = 12 s.
Avant de faire demi-tour il faut d'abord s'arrêter : à t= 9 s, il n'y a pas d'arrêt ( vitesse non nulle) , et donc pas de demi-tour.

5. Le mobile parcourt-il 180 m en 12 s ?
D1 = 10/3*3² = 30 m
D2 = 20*(9-3)= 120 m
D3 = D1 = 30 m
distance parcourue : 180 m.


II
On lâche simultanément d'une altitude h = 16 m deux objets ponctuels :
- L'un de masse M1 = 200 g sans vitesse.
- L'autre de masse M2=100 g avec une vitesse initiale verticale vers le bas de valeur Vo= 2 m/s. g=10 m/s.

1. Le temps de chute du premier vaut-il 1,6 s ?
Mouvement de chute , seul le poids travaille.
On choisit un axe vertical, orienté vers le bas, l'origine est à l'altitude h= 16 m par rapport au sol.
Premier objet : vitesse V1 = gt= 10 t ; distance parcourue D1 = ½gt² = 5 t²
Second objet : V2 = 10t + 2 ; D2 = 5 t² + 2t
Durée de la chute du premier : t²= 16/5 = 3,2 ; prendre la racine carrée : 1,79 s.

2. A l'instant t= 0,5 s, la vitesse du premier vaut-elle 5 m/s ?
A t = 0,5, la vitesse du premier est : V1 = 5 m/s.

3. A l'instant t= 0,5 s, la vitesse du second vaut-elle 7 m/s ?
A t = 0,5 s la vitesse du second vaut : V2 = 10*0,5 +2 = 7 m/s

4. La vitesse d'arrivée au sol du second vaut-elle 18 m/s ?
Durée de la chute du second : 16 = 5 t²+2t
Résoudre l'équation du second degré : t =1,6 s
vitesse : 10*1,6 +2 = 18 m/s.

5. La vitesse d'arrivée au sol du premier vaut-elle 16 m/s ?
Durée du parcours : 1,79 s
A t = 1,79 s, la vitesse du premier est : 1,79*10 = 17,9 m/s.
Or il y a seulement chiffres significatis dans les données : donc V arrondie à 18 m/s.

III
A, B, C sont trois satellites de la Terre évoluant à des distances respectives D1, D2, D3 du centre de la Terre sur des orbites circulaires parcourues avec des périodes respectives T1, T2, T3. On note V1, V2, V3 les vitesses respectives des satellites.
On donne D1= 3 D2 et T2 / T3 = 8/27.

1. D1/D3 vaut-il 4/3 ?


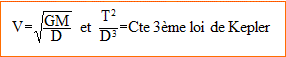
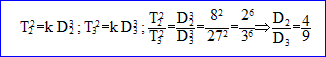
d'où D1/D3 = 4/3.

2.T1/T3 vaut-il : 8 racine carrée (3) / 9 ?


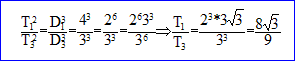
3. V1/V3 vaut-il : racine carrée (3) / 2 ?


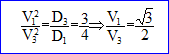
4. V1/V2 vaut-il : racine carrée (3) / 3 ?


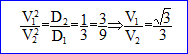
5. Les trois satellites ont-ils une accélération tangente à leur trajectoire ?
Les satellites ne sont soumis qu'à la force de centripète exercée par la Terre.
D'après la seconde loi de Newton, l'acélération est centripète, dirigée vers le centre de la Terre.